This discussion is based on a relative “best-case” experiment – expected variations if everything is “ideal”. A worst-case analysis obviously has a different objective.
One of the major disruptions in this analysis is the effect of the reflecting surface. Even considering atmospheric effects such as variations in scattering elements, the most significant loss of beam intensity occurs at the reflecting surface. Fortunately, this is a common-mode affect; creating a proportionally identical loss in both measurement channels. This is most noticeably apparent in the magnitude of the received signals – limiting the useful dynamic range of this measurement and increasing signal noise.
The calculations assumed perfect and normal reflection from a planar surface. In reality, the return signal is affected by many variations in the earth surface. Many experiments are conducted over the American southwest deserts: bare sand has a reflection coefficient of roughly 0.4. Snow would reflect perhaps 85%, while a deep pine forest may only have a reflection coefficient of 0.1. With a beam diameter of 4 m, seemingly minor topography changes would change the angle of reflection even with uniform materials. It seems likely that a strong correlation of measured data to surface topography exists for any individual measurement.
One might imagine the reflected beam front appearing as shown; still assuming normal reflection, the lightest area representing photons that might be detected, the darker regions representing photons lost to the signal.

Roughness of the surface – be it flat ice or leafy forest – as well as the offset angle of the reflection will modify the photon count. From an instrumentation point-of-view, the dynamic range will vary with surface conditions. The instrument can lose resolution by accepting a wide range of intensities, or can be configured to “optimize” detection based on the reflecting surface characteristics – flying over an ocean will require a different optimized range than will extensive forest regions – or cities.
If the assumptions of the differential-mode aspects of the measurement are valid to the degree desired, reflectivity should be “identical” for both the ON and OFF channels and the effect is simply a lessening of the common-mode signal strength. However, the instrumentation needs to consider the electronic parameter of common-mode rejection. Consideration of electronic system design considerations is beyond the purpose of this discussion, but maintaining the integrity of the separation of common-mode magnitude from the differential-mode information becomes significant when attempting to resolve small signals.
Is the difficulty in proper interpretation to be deferred until post-flight analysis or to be dealt with by adding correction networks to the optics circuitry? Either is feasible.
Not Measured
It is important to note what is not measured.
The only thing that is measured is the photodiode current related to the number of photons at the photodetector. All else is interpretation by scaling.
It is a fairly reasonable assumption that the current which is created by the instantaneous optical intensity (in units of watts/meter2) impinging the face of the photodiode [1] (with detection area in units of meter2) has a linear relationship (in units of amps/watt) to the variation in number of photons – if the optical intensity range matches the detector dynamic range. This is true except at the limits of the detector dynamic range: dark current limits the low end; saturation current limits the high end. It is best to keep the expected signal range inside perhaps about 10x dark current and 80% of saturation current.
There is no difference in photons having different path lengths – due to repeated scattering perhaps – within the detection range of the photodiode. The detector does not count absorbed photons; it does not correlate time; it counts received photons from whatever source. The detector will not differentiate between a thin region of high concentration of absorbing/scattering material and a thicker region of lower concentration.
The measurement relates the difference in received photons of the absorption to those of the non-absorption wavelengths. The detector itself can not differentiate between photons of these (close but not equal) wavelengths.
To re-iterate:
represents the effective absorption cross-sectional area of each photon within thickness of dz – initially assumed equal for all dz. Z is the total path length (2x altitude) and
CO2 is the number of absorbing molecules in volume
dz. The project attempts to measure
CO2 by inferring the change in
CO2 as compared to the nominal
CO2nom when referenced to non-absorbing wavelengths. This is done by measuring the electrons which are generated by the photons of the absorbing and non-absorbing wavelengths
The detector will require a minimum optical power to provide a usable measurement; it also has a maximum limit of input optical power beyond which the detector will possibly be destroyed. For all intents and purposes, the dark current limits the low end; there are no negative photons which will reduce current. The upper signal limit is defined by distortion and the risk of physical damage.
These limits define the detector dynamic range; the laser transmit power and allowable intensity losses need to be matched with a detector to maximize measurement dynamic range and accuracy.
All else is secondary.
[1] A photodetector PD with diameter of 200mm has a detection area of 31.4E-9 m2. With a responsivity of 1 A/W, an intensity of 31.8 mW needs to impinge the PD to generate a signal current equal to a dark current of 1 nA. If the dark current increases to 100 nA with APD gain of 20 (at R = 10A/W), then 318 mW is necessary. A comparison chart of various PDs is presented in a later section.
It should be considered that a non-APD device may have better sensitivity for less laser power and less noise than the APD structure.
Geometrical Range Measure
The complexity of determining optical path length to the necessary accuracy may be illustrated by applying some basic ranging calculations used to determine altitude. Alternative methods may be feasible.
The time factor of the basic range is defined by:
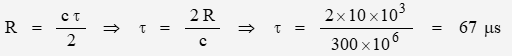
… where τ is the length of time the beam takes to travel from transmitter to receiver. is range and
is speed-of-light (better: velocity in free space).
Range resolution is defined by where a desired range resolution
within range R requires a bandwidth BW.
The basic system function was defined as with sensitivity
For to be determined to 0.25%, uncertainty in z should be roughly 1/10 to minimize uncertainty due to range. If so, 0.025% of 10 km is 2.5 m
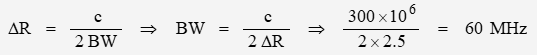
If stepped-frequency techniques are used (as an example):
To prevent aliasing, the product of time and frequency increment must be equal or less than 1 (a value of 1 assumes no motion; a value less than 1 allows for Doppler shift due to changes in relative velocity between transmitter and target. A value greater than 1 introduces aliasing)

Since bandwidth BW is equivalent to the product of number of steps and frequency increment
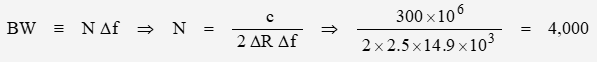
To measure altitude to sufficient resolution requires a ranging system with bandwidth of 60 MHz having a minimum of 4000 steps at frequency increments of 15 kHz. This is not truly feasible as a combined function in a unified system measuring subtle changes in amplitude and is best accomplished with a separate range detection instrument.
That’s all for now.
Next 9: Photodiodes & Signal Range
