PTAT – Dave McGlone

Proportional-To-Absolute-Temperature

“Absolute temperature” being degrees Kelvin. Conveniently, degrees Celsius/Centigrade overlaps the Kelvin scale with identical magnitude: 1K = 1^oC

I have elsewhere presented the diode equation as:

$\begin{displaymath}I_D \; = \; I_s \, \left[ \, exp \left(\, \frac{q \, V_D}{\, n \, k \, T \, } \,\right) \, - \, 1 \, \right]\end{displaymath}$

and demonstrated that the “minus 1” term may usually be neglected. Doing so, I can write the diode equation as:

$\begin{displaymath}V_D \; = \; \frac{\, n \, k \, T \,}{q} \, ln \left( \frac{\, I_D \,}{I_s} \right)\end{displaymath}$

The parameter “n” is often assumed a value of “1” although a value of 1.3 may be a better approximation. I won’t concern myself with that at the moment …

The concept of “thermal voltage” will appear fairly often and is defined:

$\begin{displaymath}V_T \; = \; \frac{\, k \, T \,}{q}\end{displaymath}$

$k$ is Boltzmann’s constant (~1.381 $\text{e-23}$ J/K), q is electron charge (~1.602 $\text{e-19}$ C), and T is the junction temperature in K. k and q are physical constants whose ratio is 86.17 $\text{e-6}$ V/K. At “room” temperature (300K = 27^oC = 80^oF), $V_T$ = 25.85 mV.

Note: The temperature parameter in SPICE is used as the junction temperature. I often define T at 40^oC: equal to 313K or 104^oF. If defining in kelvin, I use 315K. These are more likely junction temperatures for an active network in idle state. YMMV of course.

I want to examine the term $I_s$ . Known as the “saturation” current in the SPICE model and sometimes expressed as $I_o$ , the term may be expressed in terms of current density: $I_s \, = \, J_s \, A$ , where $J_s$ is the current density through the junction and $A$ is the effective area through which the current flows.

Consider this network:

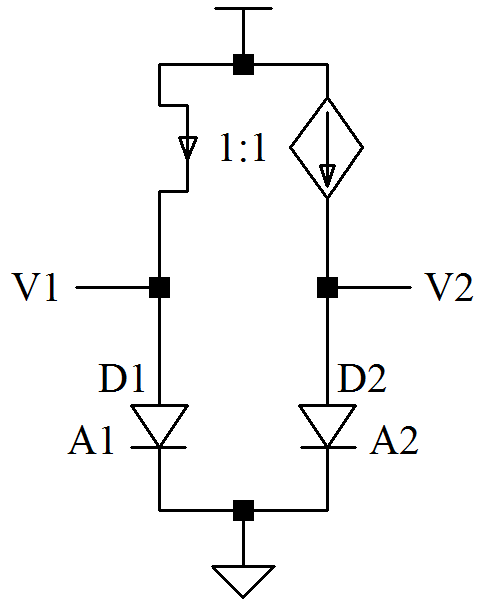
Two matching diodes built on the same process in parallel branches with identical junction currents (via the ideal P-polarity current mirror) and at equal temperature.

$\begin{displaymath}\begin{align}V_{D1} \; &= \; \frac{\, n \, k \, T \,}{q} \, ln \left( \frac{I_D}{\, J_s \, A_1 \,} \right) \; \; = \; \; V_1 \; &= \; V_T \, ln \left( \frac{I_D}{\, J_s \,} \right) \\\\V_{D2} \; &= \; \frac{\, n \, k \, T \,}{q} \, ln \left( \frac{I_D}{\, J_s \, A_2 \,} \right) \; \; = \; \; V_2 \; &= \; V_T \, ln \left( \frac{I_D}{\, J_s \, A \,} \right)\end{align}\end{displaymath}$

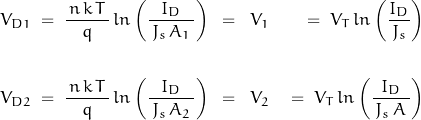
Taking the difference in voltages …

$\begin{displaymath}V_1 \, - \, V_2 \; = \; V_T \left[ \, ln \left( \frac{I_D}{\, J_s \,} \right) \; - \; log \left( \frac{I_D}{\, J_s \, A \,} \right) \, \right] \; \; = \; \; V_T \left[ \, ln \frac{\left( \frac{I_D}{\, J_s \,} \right)}{ \, \left( \frac{I_D}{\, J_s \, A \,} \right) \, } \right]\end{displaymath}$

or:

$\begin{displaymath}V_1 \, - \, V_2 \; = \; V_T \; ln (A_2) \; \; \Rightarrow \; \; T \; \times \; 86.17\text{e-6} \; ln (A_2)\end{displaymath}$

A voltage linearly proportional to temperature T (assuming effective $A$ is constant).

In developing “matching” components of different sizes, it is often useful to define a “unit” component and build arrays of identical pieces. For example, if I were to build a 3 $\times$ 3 array of diodes, I could easily develop a 1:8 relationship of junction areas. The voltage difference would then be:

$\begin{displaymath}\Delta V \; = \; 86.17\text{e-6} \; T \; ln (8) \; = \; 179.19\text{e-6} \; T \; \; \Rightarrow \; \; 53.76 \; mV \, \vert_{300K}\end{displaymath}$

The effective temperature coefficient:

$\begin{displaymath}\frac{\, \partial \, V \, }{\partial T} \; = \; 86.17\text{e-6} \, ln (8/1) \; \approx \; 179\,ppm\end{displaymath}$

The primary errors would be due to mismatches in branch currents, leakage currents, and device matching.

A companion article may be read here: pn-Junction Temperature Coefficient

That’s good for now.

Leave a Reply Cancel reply