Subsurface Detection 3 – Half-Space Model

The receiver is co-planar with the dipole source on a surface (z = 0). In the simplest manifestation, the model consists of a homogeneous conductive material having a planar interface with a non-conductive free space – the surface of a uniform “earth”. The model may be made more complex according to analysis requirements. A presumption of equivalency to the transmission model of the earth is made for this analysis.

Quasi-stationary source field conditions are assumed; i.e., a single frequency sinusoidal magnetic dipole located at the coordinate origin is considered the input stimulus. The interface boundary is the X-Y plane defined for z = 0.

Define the system functions in cylindrical coordinates so that $\rho \, = \, \sqrt{\,x^2 \, + \, y^2 \,}$ , where z = 0 and $\rho$ = {x, y} at the interface surface. These functions are valid $^*$ for distances $\rho$ << $\delta$ , where $\delta$ is the skin depth. The X-Z cross-section of the system geometry was illustrated in Figure 1 of Part 2, where the X-Y plane (Z = 0) represents the interface plane.

The z-component of a magnetic vector potential, $A$ , is expressed as:

$\begin{displaymath} A_z \; = \; -\jmath \, \omega \, \dfrac{\mu \, M}{\, 2 \, \pi \, k^2 \,} \, \dfrac{1}{\, \rho^3 \,} \, \left[ \, 1 \, - \, \left( \, 1 \, - \, \jmath \, k \, \rho\, \right) \, \mathbb{e}^{\jmath \, k \, \rho} \, \right] \end{displaymath}$

where k is the radial wavenumber relating material parameters to the half-space model.

k is defined in the following manner:

$\begin{displaymath} \begin{align} k^2 \; &= \, \mu \, \varepsilon \, \omega^2 \, - \, \jmath \: \omega \, \mu \, \gamma \\ \\ k \; &= \, \jmath \: \sqrt{\, - \jmath \: \mu \, \omega \, \mu \, \gamma \,}$ for $\omega \, \varepsilon \, << \, \gamma \end{align} \end{displaymath}$

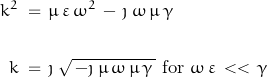
ω represents the transmission frequency in radians/s, $\mu$ represents the permeability of the material ( usually taken to be $\mu_o$ ), ε is the material dielectric permittivity, and γ is the conductivity of the medium.

In the half-space model, the finite medium interfaces with free-space in such a way as the free-space magnetic field vectors are normal to the half-space boundary; i.e., only the vertical magnetic field component ( $B_z$ ) manifests itself at the surface. This turns out to be a fair approximation of the earth-air interface (or any other conductive material interfacing with air or vacuum).

The half-space magnetic field components may now be expressed:

$\begin{displaymath} \begin{align} B_\rho \; &= \; \dfrac{1}{\, \jmath \, \omega \,} \, \dfrac{\partial^2 \, A_z}{\, \partial \rho \, \partial z \,} \\ \\ &= \; -M \, \dfrac{\mu}{\, 4 \, \pi \, \rho^3 \,} \, k^2 \, \rho^2 \, \left[\, \mathbb{I}_1 \left(\dfrac{\, \jmath \, k \, \rho \,}{2} \right) \, \mathbb{K}_1 \left(\dfrac{\, \jmath \, k \, \rho \,}{2} \, \right) \; - \; \mathbb{I}_2 \left(\dfrac{\, \jmath \, k \, \rho \,}{2} \, \right) \, \mathbb{K}_2 \left(\dfrac{\, \jmath \, k \, \rho \,}{2} \, \right) \, \right] \\ \\ &\Rightarrow \; 0 \; for \; z \, = \, 0 \end{align} \end{displaymath}$

where $\mathbb{I}_x$ and $\mathbb{K}_x$ represent the appropriate Bessel functions of the indicated order.

and the vertical component:

$\begin{displaymath} \begin{align} B_z \; &;= \; \dfrac{1}{\, \jmath \, \omega \,} \, \left(\, k^2 \, A_z \, + \, \dfrac{\, \partial^2 A_z \,}{\partial z^2} \, \right) \\ \\ &= \; -M \, \dfrac{\mu}{\, 2 \, \pi \, \rho^3 \,} \, \dfrac{1}{k^2 \, \rho^2} \, \left[\, 9 \, - \, \left( \, 9 \, + \, \jmath \; 9 \, k \, \rho \; - \; 4 \, k^2 \, \rho^2 \, - \, \jmath \, k^3 \, \rho^3 \, \right) \, \mathbb{e}^{\, -\jmath \, k \, \rho} \, \right] \end{align} \end{displaymath}$

The E-field only has a single component coincident with the magnetic vector potential; taken to be in the $\phi$ direction, parallel to the interface x-y plane.

From $E \, = \, \nabla \, \Phi \, - \, \dfrac{\, \partial A \,}{\partial t}$ and assuming insignificant free charge within the exploration volume, the electric field $\phi$ -component is found to be:

$\begin{displaymath} E_\phi \; = \; -\jmath \, \omega \, \mu \, \dfrac{M}{\, 2 \, \pi \, \rho (x,y)^3 \,} \, \dfrac{1}{\gamma_o \, \rho (x,y)} \, \left\{\, 3 \, - \, \left[ \, 3 \, + \, \jmath \; 3 \, k \, \rho (x,y) \; - \; 4 \, k^2 \, \rho (x,y)^2 \, \left] \, \mathbb{e}^{\, -\jmath \, k \, \rho} \, \right\} \end{displaymath}$

The vertical component of the primary magnetic field $B_z$ are calculated at the surface as shown in the following figure. The magnetic dipole moment is 2800. The axes are nT vs. meters

The range of detection extends to about 140 m in this free-space model. Of course, the earth subsurface is not free-space.

Part 2
Part 4

That’s good for now.

$^*$ For reference, in free space: 300MHz ⇒ λ = 1 m. 300kHz ⇒ λ = 1 km and 30 kHz ⇒ λ = 10 km. These values are dependent on the relative permittivity when travelling through a finite media and are considerably different in regions with finite conductivity.

For reference, in free space: 300MHz ⇒ λ = 1 m. 300kHz ⇒ λ = 1 km and 30 kHz ⇒ λ = 10 km. These values are dependent on the relative permittivity when travelling through a finite media and are considerably different in regions with finite conductivity.

A derivation of the magnetic dipole may be found here

$^*$ For reference, in free space: 300MHz ⇒ λ = 1 m. 300kHz ⇒ λ = 1 km and 30 kHz ⇒ λ = 10 km. These values are dependent on the relative permittivity when travelling through a finite media and are considerably different in regions with finite conductivity.