Let’s assume an ideal and homogeneous half-space. The electromagnetic fields created from a magnetic dipole have cylindrical symmetry about the dipole axis within the media. The dipole is placed at the origin and directed along the z-axis as shown in Figure 1 with the resulting field vectors as shown. Vector ![]() is measured; it is the distortion of this vector which contains the desired information. The magnetic dipole is formed with a current loop. The geometry of a possible anomaly is illustrated here, but the discussion of secondary fields is deferred for now.
is measured; it is the distortion of this vector which contains the desired information. The magnetic dipole is formed with a current loop. The geometry of a possible anomaly is illustrated here, but the discussion of secondary fields is deferred for now.
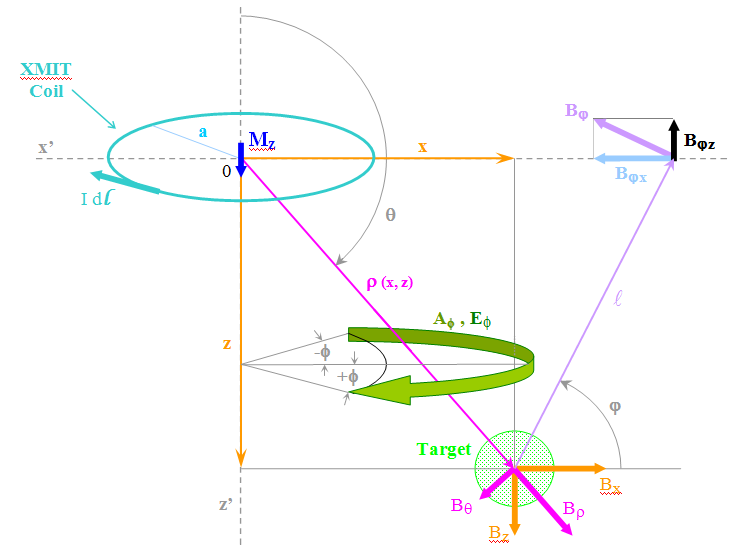
The x-y plane elements are distorted in the illustration for clarity. The y-axis is normal to the illustration.
The far-field free-space magnetic dipole are valid for ![]() where “
where “![]() ” is the transmit coil radius.
” is the transmit coil radius.
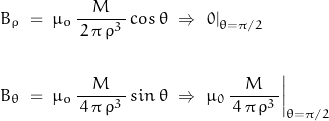
From ![]() , the vertical field component is expressed as:
, the vertical field component is expressed as:
![]()
where ![]() is the transmitted source field represented as a magnetic dipole.
is the transmitted source field represented as a magnetic dipole.
Defining ![]() in the time-domain as
in the time-domain as ![]() , the following expressions define the primary magnetic field for a homogeneous media in which
, the following expressions define the primary magnetic field for a homogeneous media in which ![]()
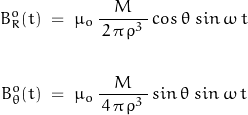
A vortex electric field rotates about the dipole axis as:
![]()
where ![]() which are the source dipole parameters.
which are the source dipole parameters.
The ![]() and
and ![]() terms are separated for clarity, but arise from
terms are separated for clarity, but arise from ![]() . Equipotential force contours of the magnetic field component
. Equipotential force contours of the magnetic field component ![]() and the electric field component
and the electric field component ![]() are shown for a single quadrant cross-section of free-space in Figure 2.
are shown for a single quadrant cross-section of free-space in Figure 2.
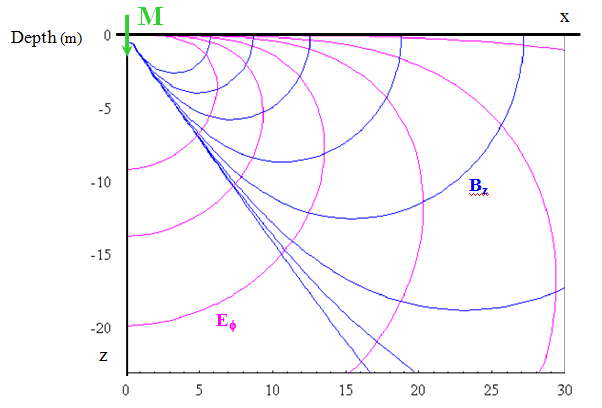
These field lines represent equipotential contours within a homogeneous half-space created by a surface magnetic dipole M.
That’s good for now.
![]()