Skin Depth & Coated Wire 3 Inductance

Internal DC Inductance

Keep it “simple”; an infinite straight length along vector z of a circular conductor of radius R carrying uniform current I. The return path is infinitely far away. This is math, not reality …

The magnetic field created by this current is both internal and external – I want to examine the inductance related to the internal fields. The field is assumed constant with z; the lines of magnetic flux are concentric about the center line of the conductor.

Inductance L is defined by:

$\begin{displaymath}L\;\equiv\;\frac{\,\Phi\,}{I}\end{displaymath}$

The magnetomotive force $\mathcal{F}$ around a closed path is equivalent to the current enclosed by the path:

$\begin{displaymath}\mathcal{F}\;\equiv\;\int_S\,\mathcal{H}\cdot dS\end{displaymath}$

where $\mathcal{H}$ is the magnetic field intensity.

I want to find the field intensity at any distance $r$ from the conductor center. The field is symmetrical; I can use “distance from center” equally in Cartesian or cylindrical coordinates. The use of Cartesian “ $r$ ” as a variable is less confusing that the cylindrical ρ.

The magnetic field intensity at any distance x from center is $\mathcal{H}_x$ . The field is constant and symmetrical about the axis therefore:

$\begin{displaymath}\mathcal{F}\;=\;H_r\,\int_S\, dS\end{displaymath}$

where the integration becomes:

$\begin{displaymath}\int_S\, dS\;=\;2\pi\,r\end{displaymath}$

giving:

$\begin{displaymath}H_x\,2\pi\,r\;=\;H_r\,I_r\;\;\Rightarrow\;\;H_r\;=\;I_r\,\frac{1}{\,2\pi\,r\,}\end{displaymath}$

Because the current density is uniform:

$\begin{displaymath}\frac{I_r}{\,\pi\,r^2\,}\;=\;\frac{I}{\,\pi\,R^2\,}\;\;\Rightarrow\;\;I_r\;=\;I\,\frac{\,\pi\,r^2\,}{\,\pi\,R^2\,}\;\;\Rightarrow\;\;I_r\;=\;I\,\frac{\,r^2\,}{\,R^2\,}\end{displaymath}$

By substitution:

$\begin{displaymath}H_r\;=\;\;\left(\,I\,\frac{\,r^2\,}{\,R^2\,}\,\right)\,\left(\,\frac{1}{\,2\pi\,r\,}\,\right)\;\;\Rightarrow\;\;I\,\frac{r}{\,2\pi\,R^2\,}\end{displaymath}$

So the flux density at some radius $r$ is:

$\begin{displaymath}\mathcal{B}_r\;=\;\mu\,H_r \;\;\Rightarrow\;\;\mu_r\,\mu_o\,I\,\frac{\,r\,}{\,2\pi\,R^2\,}\end{displaymath}$

We just went through this in the previous section … in terms of $\mathcal{B}$ though. Almost the same thing – so far.

I hope I got the same results this time …

The total flux linkage inside the conductor is found by integrating from the conductor axis to the conductor surface:

$\begin{displaymath}\psi_{int}\;=\;\int_0^r \,d\psi \;=\;\int_0^r \,\mu_r\,I\,\frac{\,\mu_o\,r^3\,}{\,2\pi\,R^4\,}\,dr\;\;=\;\;\frac{\,\mu \, I\,}{\,8\,\pi\,}\quad Wb-t/m\quad \;\;\Rightarrow\;\;\psi_{int}\;=\;\frac{I}{\,2\,}\,\times 10^{-7}\;\;\;for\;\mu\;=\;\mu_o\end{displaymath}$

For constant current (DC), the inductance per metre is therefore:

$\begin{displaymath}L\;\equiv\;\frac{\,\Phi\,}{I}\;\;\Rightarrow\;\;\frac{\,\frac{1}{\,2\,}I\times 10^{-7}\,}{I}\;\;=\;\;50\,nH/m\end{displaymath}$

However, when the current is not constant and skin effect is considered, this solution is not adequate.

Internal AC Inductance

I seek an expression for internal inductance which accounts for changes in frequency – how does inductance change as skin depth changes?

$L_{AC}\;=\; L_{DC}\,\times\,\mathit{f}_{adjustment}$

Kelvin Functions

I study nothing new … William Thomson – “Lord Kelvin” – studied “skin effect” during the 1850s when working on cross-Atlantic telegraph lines. A specific form of Bessel Function, the Kelvin Functions, came about from Thomson’s work in solving the expression:

$\begin{displaymath}\frac{1}{\,r\,}\frac{\partial}{\,\partial r\,}\,\left(\,r\,\frac{\,\partial{\textnormal{J}}\,}{\partial r}\,\right)\;=\;\frac{\,4\,\pi\,\mu \,}{\rho}\frac{\,\partial{\textnormal{J}}\,}{\partial t}\end{displaymath}$

Noting that alternating current can be expressed as:

$\begin{displaymath}\textnormal{J}(r,t)\;=\;R(r)\,\mathit{e}^{+\mathit{j}\omega t}\end{displaymath}$

He arrived at a solution in the form of a complex Bessel Function:

$\begin{displaymath}R(r)\;=\;C_1\,I_o\,\left(k r \sqrt{\,\mathit{j}\,}\right)+C_2\,K_o\,\left(k r \sqrt{\,\mathit{j}\right)\,}\end{displaymath}$

where $C_1$ and $C_2$ are constants of integration and k is a material parameter.

Solutions to problems involving electromagnetic wave propagation in cylindrical structures usually involve the use of a variety of Bessel Functions. I avoid the detailed discussions of these functions other than noting that the functions I and K are modified Bessel functions of the 1st and 2nd kind respectively.

The series expansion for function $I_o(\mathit{j}\,x)$ can be separated into real and complex components; Kelvin defined the terms as:

$\begin{displaymath}I_o(\mathit{j}\,x) \;=\; ber(x)\,=\,\mathit{j}\,bei(x)\end{displaymath}$

Similarly for the Bessel Function $K_o$ :

$\begin{displaymath}K_o(x) \;=\; ker(x)\,=\,\mathit{j}\,kei(x)\end{displaymath}$

Per Abramowitz & Stegun, the Kelvin Functions (in Sect 9.9) are given as:

$\begin{displaymath}ber_\nu (x)\,+\,\mathit{j}bei_\nu (x)\;=\,\textnormal{J}_\nu \left(\,x \, \mathit{exp}[\mathit{j}\,3\pi/4]\,\right)\end{displaymath}$

where $\nu$ and x are real, and n is 0 or a positive integer.

For the 0th-order functions, the following series expansions apply:

$\begin{displaymath}ber_o (x)\;=\;ber(x)\;=\;1\,+\, \sum_{k\ge1} \,\frac{(-1)^k}{\,[\,(2k)!\,]^2\,}\,\left(\,\frac{x}{\,2\,}\,\right)^{4k}\end{displaymath}$

$\begin{displaymath}bei_o (x)\;=\;bei(x)\;=\;\sum_{k\ge 0} \,\frac{(-1)^k}{\,[\,(2k\,+\,1)!\,]^2\,}\,\left(\,\frac{x}{\,2\,}\,\right)^{4k+2}\end{displaymath}$

Although mathematical analysis programs have advanced to the point where the functions may be evaluated directly without resorting to series approximations (in most cases).

So an expression for the internal inductance over frequency is obtained:

$\begin{displaymath}L_i\;\;=\;\;\frac{\,4\,}{x}\; L_{DC}\; \frac{\,\mathit{bei}(x)\,\mathit{bei}'(x)\;+\;\mathit{ber}(x)\,\mathit{ber}'(x)\,}{\mathit{bei}(x)^2\;+\;\mathit{ber}(x)^2}\end{displaymath}$

$\begin{displaymath}\textnormal{\small{where }}x\;=\; \frac{d}{\,\delta\,\sqrt{2}\,}\quad\textnormal{\small{and}} \;\textnormal{\small{d is diameter in m}}\end{displaymath}$

Manipulating the first terms:

$\begin{displaymath}\frac{\,4\,}{x}\; L_{DC}=\;\;\frac{\,4\,\delta\,\sqrt{\,2\,}\,}{d}\; L_{DC}\;\Rightarrow\;\frac{\,4\,\delta\,\sqrt{\,2\,}\,}{d}\; \frac{\mu}{\,8\,\pi\,}\;\Rightarrow\;\frac{\,\sqrt{\,\mu\,}\,}{\,d\,\sqrt{\,\pi^3\,f\,\rho\,}}\end{displaymath}$

Defining the derivatives of the Kelvin functions:

$\begin{displaymath}bei_o' (x)\;=\;\frac{\,bei_1(x)\,-\,ber_1(x)\,}{\sqrt{\,2\,}} \quad\quad ber_o' (x)\;=\;\frac{\,bei_1(x)\,+\,ber_1(x)\,}{\sqrt{\,2\,}}\end{displaymath}$

And substituting gives a delightful expression for the internal inductance of a straight wire:

$\begin{displaymath}L_i\;\;=\;\;\frac{\,\sqrt{\,\mu\,}\,}{\,d\,\sqrt{\,\pi^3\,f\,\rho\,}}\;\frac{\,\mathit{bei}(x)\,[\,\mathit{bei}_1(x)\,-\,\mathit{ber}_1(x)\,]\;+\;\mathit{ber}(x)\,[\,\mathit{bei}_1(x)\,+\,\mathit{ber}_1(x)\,]\,}{\sqrt{\,2\,}\;[\mathit{bei}(x)^2\;+\;\mathit{ber}(x)^2]} \quad H/m\end{displaymath}$

Plotting inductance per unit length over depth from surface for several frequencies:

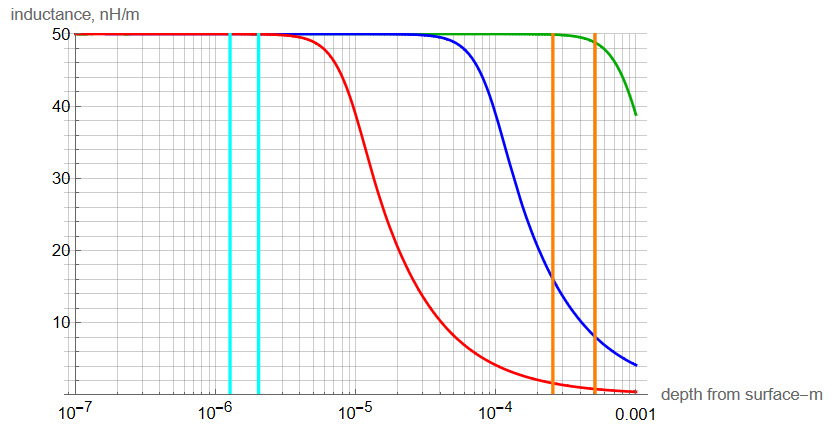
Inductance vs. Depth from Surface
GRN: 100kHz; BLU: 10MHz; RED: 1GHz
CYN: 1.27μm; 2.03μm; ORG: radius (0.255mm); diameter (0.511mm)

Previous: Part 2

Next: Part 4

Leave a Comment Cancel Reply