I left off last time after determining the numerical limits of the Bessel term but determined the slope of the solid conductor function became asymptotic to the tubular functions.
I won’t need so much math on this post – I primarily concentrate on the differences related to the wire coatings.
Recall the physical properties of the three materials of interest:
| Material |  |  |  |
| Copper Cu | 0.999994 | 59.595e6 S/m | 16.78 n m |
| Silver Ag | 0.99998 | 63.012e6 S/m | 15.87 n m |
| Nickel Ni | 100-600 | 14.430e6 S/m | 69.30 n m |
Examination of the Bessel argument shows silver and copper essentially identical but nickel having a significant difference
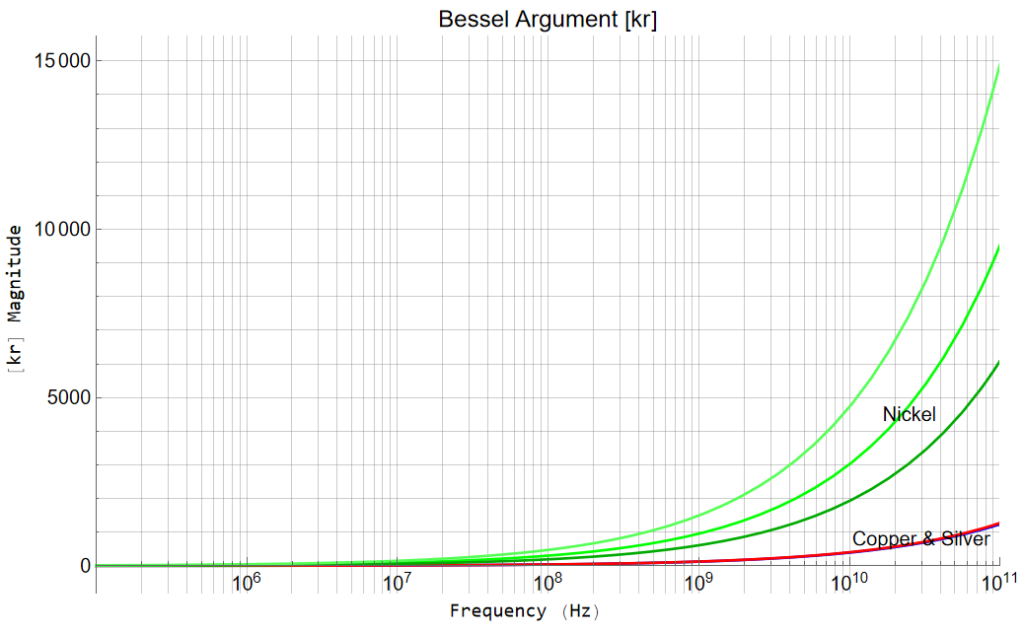
Nickel has a wide reported range of relative permeability (100 – 600). The two extremes are plotted along with the geometric mean (
). Copper and silver are essentially identical. A relative permeability of 1 was used for both although both are very slightly diamagnetic. The major difference between the two is conductivity (16.8 for copper; 15.9 for silver. 69.3 for nickel)
“0” frequency is a mathematical concept. In an experiment: Turn on equipment Mon at 8AM, leave on during week, turn off Fri at 4PM. That’s 104 hours or 374,400 seconds … or 2.67e-6 Hz. A one year cycle is 31.7 nHz
I think we’ll skip the minutiae here …
So here I combine all the information from the previous section (4a) with the material data from this page to arrive at this busy plot.
Of importance are the diagonal lines representing skin depth (GRY), the horizontal lines representing the AWG24 conductor radius (BLK) and conductor plating thicknesses (ORG).
The copper and silver skin depths become less than the radius at about 70kHz; nickel crosses at just over 1 kHz. Skin depth becomes less than the plating thickness for nickel at 15 MHz; copper and silver at 2GHz.
Is this even an issue? This is wire intended for a data bus. Considering both harmonic content of digital signals and transmission frequencies … one could become curious.
