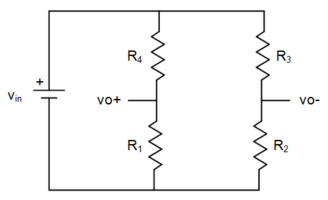
The Wheatstone Bridge is a simple circuit capable of making very accurate measurements. The basic network was actually proposed in the 1830s by Samuel Christie but named after Charles Wheatstone who publicly presented it – as Christie’s work – in 1843. It remains the basis for many transducer interface networks to this day.
![]()
![Rendered by QuickLaTeX.com \begin{displaymath}V_{out} \; = \; V_{in} \, \left[ \, \frac{ \frac{R_1}{\, R_4 \, } \, - \, \frac{R_2}{\, R_3 \, } }{\, \left( \, 1 \, + \, \frac{R_1}{\, R_4 \, } \, \right) \, \left( \, 1 \, + \, \frac{R_2}{\, R_3 \, } \, \right) \, } \, } \, \right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-36fe83d387c98d032667e948bfaf06f2_l3.png)
The system is in balance when Vout = 0 … or when (R1/R4) = (R2/R3). Note that this is a ratiometric comparison. Note also it is non-linear.
Consider the situation where R1 = R2 = R3 = R1 = R but allow R1 to vary by ΔR due to some influence … perhaps temperature, strain, or some such.
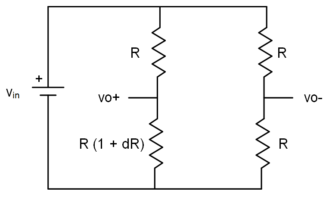
The bridge expression may now be expressed:
![]()
![]()
The absolute value of R is not part of the expression.
The sensitivity of function y to a change in parameter x of that function is defined:
![]()
which gives the sensitivity of the output to a change in R1 of:
![]()
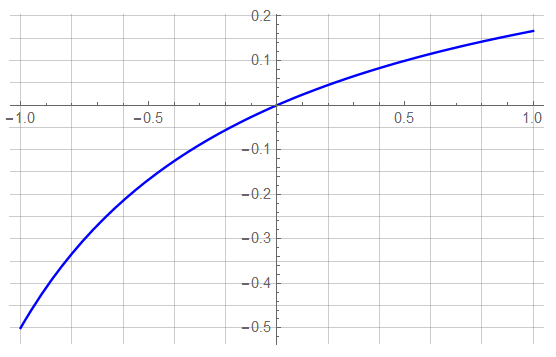
Follows is a plot for ![]() R between -100% and +100% ( R1 = 0 → +2 for R = 1 ). Vout has the following non-linear response:
R between -100% and +100% ( R1 = 0 → +2 for R = 1 ). Vout has the following non-linear response:
However, if ΔR is small – say no more than ±1%, the response is:
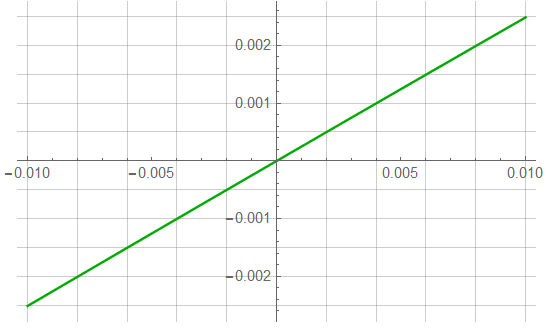
which has an ![]() value of 0.999993. A fairly linear response …
value of 0.999993. A fairly linear response …
A 10% change has an ![]() value of 0.999332; a 30% change has value of 0.993929.
value of 0.999332; a 30% change has value of 0.993929.
A plot comparing the output vs. a linear regression at 10% variation in ΔR:
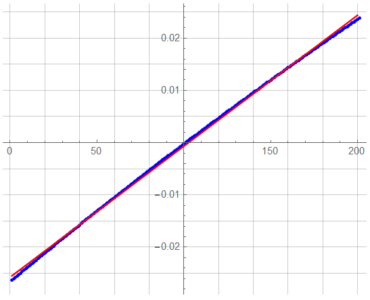
The BLU line is the output for ΔR = ±10%; the RED line is the result of the linear regression.
This is often sufficient for many measurements but some transducer variations may exceed the range where a linear assumption remains valid.
The value at ΔR = 0 is -0.0257 … a perhaps unacceptable error of 2.6%. This is the same magnitude error (to 2 places) at the extremities as well. The true response is non-linear; a simple offset adjustment is not suitable.
It would be a stretch to assume a “linear” response for a variation of ΔR = ±100% … even if the ![]() value is 0.923227 – which suggests that an
value is 0.923227 – which suggests that an ![]() value of even 0.92 is subjectively not very good. Of course, “accurate” is relative.
value of even 0.92 is subjectively not very good. Of course, “accurate” is relative.
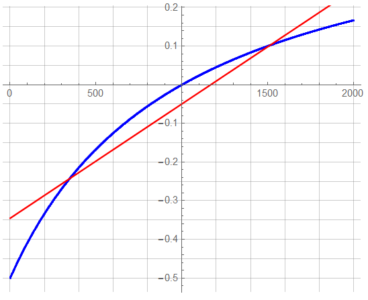
A means of linearizing the output over a wide range of ΔR is possible though.
Consider the following topology:
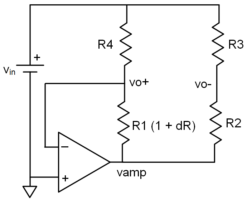
The opamp is configured such that vo+ is forced to GND through the virtual GND connection at the inverting input (recalling that the inverting input is isolated from but at the same potential as the non-inverting input). Since vo+ is at GND potential, the current through R4 is Vin/R4 … and the same current flows through R1 regardless of the value of dR.
This forces the voltage drop across R1 to be:
![]()
The opamp will force the voltage at the opamp output to be:
![]()
The current through the 2nd branch (R3/R2) is:

So that vo– may be determined from:
![]()
and
![]()
With an ideal opamp configured as previously shown and all resistors of equal value:
![]()
which, when plotted for

Keeping in mind the ratiometric balance, consider that R3 and R4 are scaled values of R1 and R2 such that R3 = R4 = x R. The output voltage is now calculated as:
![]()
The response is still linear as long as value
Possible error sources include quality of ![]() , quality of resistor matching, and opamp characteristics … but all in all, a linearization of a Wheatstone bridge over a wide variance of single-element change.
, quality of resistor matching, and opamp characteristics … but all in all, a linearization of a Wheatstone bridge over a wide variance of single-element change.

That’s good for now.