Thermal & Shot Noise Derivations

These are defined as “exact” fundamental constants by NIST

k = Boltzmann Constant = $1.380\,649 × 10^{-23}\; J/K$
q = Electron Charge = $1.602\,176\,634 × 10^{-19}\; C$

A current is defined as the movement of charge over time:

$\text{J}\; \frac{C}{\, s \,} \; = \; \frac{dq}{\, dt \,}$

Usually, current is considered as a macro effect, but here I get down into the fuzzy details.

Electrons wiggle at temperatures above absolute zero in K. Even when considered “stationary”, these wiggles form a “current”. Nyquist showed that the amplitude of the noise was determined from the sum of energies kT within a shorted transmission line connected to two equal resistances R. Over some sequence of frequency bands, each increment of frequency contributes incremental power:

$\begin{displaymath}dP \; = \; k\,T\;df\end{displaymath}$

The rms voltage of this noise is found from:

$\begin{displaymath}dV^2 \; = \; dI^2 \, (\,2\,R\,)^2\, df \; \Rightarrow \; 4 \, R^2 \; (dP/R) \; \Rightarrow \; 4\,kT\,R\,df\end{displaymath}$

This expression neglects any series capacitance in the system. Assuming an incremental parallel capacitance, the resistance term needs to be replaced with impedance:

$\begin{displaymath}Z \; = \; \dfrac{R}{\, 1\,+\,j\,\omega\,R\,C\,}\;\;\; where \;\; V^2\;\Rightarrow\;I^2\,Z^2\end{displaymath}$

Properly, a term for incremental parallel inductance should be added where:

$\begin{displaymath}Z \; = \; \dfrac{1}{\, \sqrt{\, \left(\,\frac{1}{\,R\,}\,\right)^2\,+ \; \left(\,\frac{1}{\,j\,\omega\,L\,}}\,- \, j\,\omega \,C \,\right)^2\;}}}\end{displaymath}$

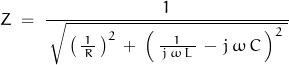
… but this won’t add additional understanding as far as macro circuits are concerned.

Back to the RC model, a generic term is added to account for amplitude variations within any incremental frequency band.

Performing the integration:

$\begin{displaymath}dV^2 \; = \; 4\,kT\,R\,\int {\dfrac{g(f)}{\, 1\,+\,(\,2\,\pi\,f\,\,R\,C\,)^2}}\,df\end{displaymath}$

Shot Noise

William Schottky’s 1918 paper: “Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern” was translated into English in 2018 to celebrate the 100th anniversary of this fundamental paper on shot noise.

“On spontaneous current fluctuations in various electrical conductors“

Schottky proposed that electrons being discrete carriers of charge, there is a “graininess” to this current due to the quantization of charge.

As an example, Schottky presented what in effect is the photoelectric effect – the transition of electron state due to the energy transfer from photon to electron.

Over a sufficient period of time, a value of average current is obtained.

Each electron contributes a momentary energy spike – a current pulse – expressed as a delta function:

$\begin{displaymath}I_n (t) \; = \; q \, \delta(t\,-\,t_n)\end{displaymath}$

Performing a Fourier transform on this pulse over time interval T:

$\begin{displaymath}I_n (t) \; = \; \frac{q}{\,T\,} \, + \, \frac{\, 2\, q \,}{T} \; \sum_M \, cos \, \frac{\,2\,\pi\,m\,(t-t_n\,)}{T}\end{displaymath}$

where “m” is the frequency element. The total current is found by the summation of the individual pulses.

$\begin{displaymath}I_T (t) \; = \; \sum_N \,I_n (t)\end{displaymath}$

The rms value of the fluctuating component is determined from:

$\begin{displaymath}\left<\,I^2\,\right> \; = \; \left(\,\frac{\, 2\, q \,}{T}\,\right)^2 \; \left<\,cos^2 \, \frac{\,2\,\pi\,m\,(t-t_n\,)}{T}\,\right>\end{displaymath}$

The phase term $t_n$ may have any value from 0 $\rightarrow$ T, by averaging over sufficient time, the $cos^2$ term goes to value of 1/2. As a result, for any frequency term m

$\begin{displaymath}d\left<\,I^2\,\right>_m \; = \; \left(\,\frac{\, 2\, q \,}{\,T\,}\,\right)^2\;\left<\frac{1}{\,2\,}\right> \; \Rightarrow \; 2 \, \left(\,\frac{\, q \,}{\,T\,}\,\right)^2\end{displaymath}$

The rms value of the total current is found by summing all individual currents. Shot noise is therefore described by the total number of current incidents over time T and the frequency indices

$\begin{displaymath},\frac{\, I_{avg} \,}{q}\,T \;\; and \;\; f\,=\,\frac{\,m\,}{T} \;\;\; \Rightarrow \;\;\; d\left<\,I^2\,\right> \; = \; 2 \, q\, I_{avg} \, df\end{displaymath}$

Noting that the average current is equivalent to DC current, the shot noise expression – as commonly stated – is shown to be:

$\begin{displaymath}I_{shot} \; = \; \sqrt{2 \, q\, I_{DC} \, \Delta f \;}\end{displaymath}$

Leave a Comment Cancel Reply