Temperature Change of Copper PCB Traces

Copper is copper, right? A great conductor. Not the best (that would be silver), but 2nd-best works … especially when […]

Copper is copper, right? A great conductor. Not the best (that would be silver), but 2^nd-best works … especially when considering cost and mechanical properties. (Why, oh why … do people pay for gold audio wires?)

From the “CRC Handbook of Chemistry & Physics“:

$\begin{array}{lr}Material & \rho \, , \, n\Omega \cdot m \\\hline1) \; silver & 15.9 \\2) \; copper & 17.1 \\3) \; gold & 24.4 \\4) \; aluminum & 28.2 \\\; tungsten & 56.0 \\\; nickel^* & 78.0 \\\end{array} \right.$

*Note: nickel is paramagnetic with relative permeability: $\mu_r\; = \; 400 - 600$

Although some form of copper is by far the most common conductor – wire – I’ve used both silver and nickel plated wires in my work. Silver’s about 10% more conductive than copper; nickel is about 4x less conductive – and has significant magnetic permeability as well. “Oops”on calculating electromagnetic propagation using the typical equations which assume a relative permeability of 1 (rather than 400 or so for nickel … when considering high-frequency skin depth on nickel-plated wire).

But let’s focus on copper. Specifically copper PCB traces.

Current through a conductor generates heat. Usually this increase in temperature is minor but with a trend towards smaller geometries and higher current densities, I’ve found this to be a significant issue at times. Fortunately for those of us lazy enough to prefer simplicity, copper resistivity is pretty linear over a very wide temperature range as shown by this plot of resistivity vs. temperature.

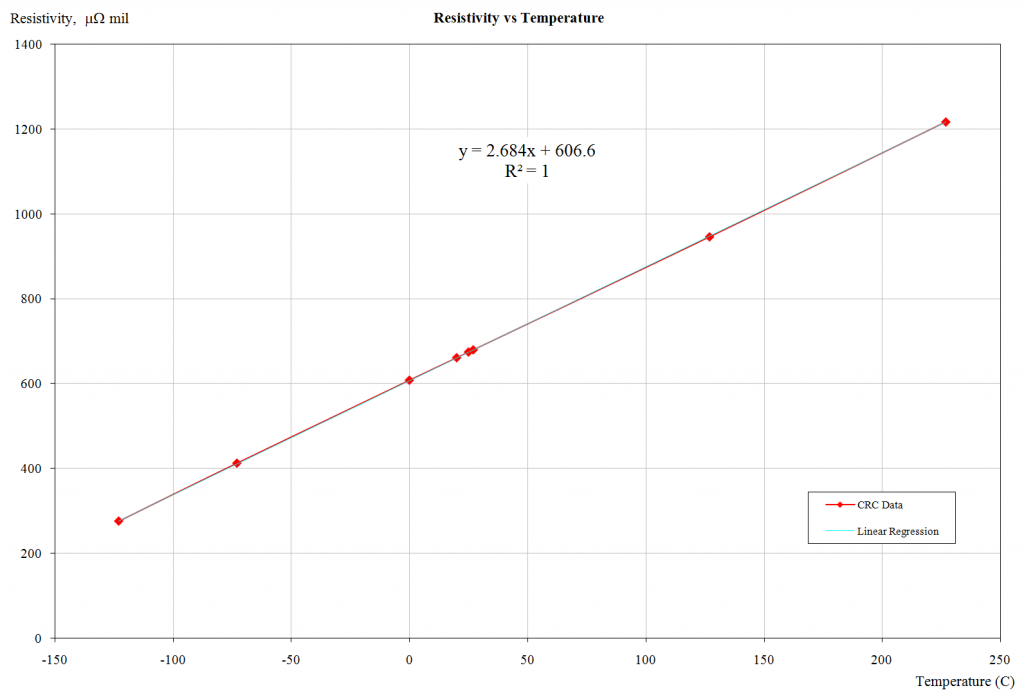
Linear regression with R² value of 1 between 150K and 500K (copper melts at 1356K). Fairly linear …

I’ve worked on circuits down to 77K (LN77 – liquid nitrogen) and up to about 600K (350°C – geothermal borehole) and the extrapolation of this curve seemed acceptable. But these are different measurement regimes with special requirements; let’s keep it reasonable.

[By the way and speaking of temperature, a rough rule-of-thumb: If you can keep your fingertip on a circuit for only a momentary count before “Ouch”, it’s running about 85°C. If “ouch” is instantaneous, you might have a thermal problem. Recall that package temperature is lower than junction temperature. If “ambient” is 25°C, I assume about 40°C (313K) for idling junction temperature.]

So the idea is to determine temperature change on a PCB trace. I used industry “standards”. I’ve not looked recently – I developed my own “calculator” several years ago … perhaps the expressions should be updated, but I suspect thermal properties have not changed much since then so I’ve not changed anything since I put these together. There are no corner corrections (corners will create a localized “hot” spot).

I would not guarantee “correctness” … but these estimations are not too far off and I still use them. It’s surprising how these seemingly little things can interfere with a good measurement (and this discussion doesn’t address thermoelectric effects such as those generated by multiple solder-copper contacts and vias). As usual, critical applications should require specific measurements on the actual circuit configuration.

The first parameter of PCB copper is weight: so many oz per square foot – often expressed simply as “1 oz copper” (which is “standard”). Depending on the PCB manufacturing house, variations between ¼ oz (maybe too light) to 4 oz (pretty heavy) may be available.

Copper thickness is 1.378 mil/oz/ft²

The resistivity of copper as a function of temperature may be expressed:

$\begin{displaymath}\rho(T) \; = \; \left[ \, 606.64 \, + \, 2.684 \times (\, T_a \, + dT \, ) \, \right] \; \; \mu \Omega \cdot \text{mil}\end{displaymath}$

The standard expressions are based on empirical measurements defined in STD IPC-275 and IPC-2221A. Internal and external traces have different coefficients. These terms define an effective cross-sectional area related to some temperature change dT in °C.

$\begin{array}{lcc}\; & Internal & External \\\hlinek & 0.0150 & 0.0647 \\b & 0.5453 & 0.4281 \\c & 0.7349 & 0.6732 \\\end{array} \right.$

$\begin{displaymath}\text{area} \; = \; \left[\, \frac{I}{\, k \, dT^b \,} \, \right]^{1/c}\end{displaymath}$

From this, the width necessary to limit dT to some defined value is as expected:

$\begin{displaymath}\text{width} \; = \; \frac{\text{area}}{\, \text{thickness} \,}\end{displaymath}$

The trace resistance is now determined from:

$\begin{displaymath}R \; = \; \rho \, \frac{\, \text{length} \,}{\text{area}}\end{displaymath}$

Let’s look at an example. I’m to use 1 oz Cu. The internal trace will carry 100 mA and there should be no more than a 1°C temperature change. The ambient temperature is 35°C and trace length is 6″.

With variables I and dT, the effective cross-section area is 13.22 mil². The trace width should be no less than 4.8 mil. The trace resistance will be 319 m $\Omega$ and voltage drop will be 31.9 mV.

Well, I’ve kept the change in temperature low enough but that’s a large voltage drop. Try again.

Keeping the 6″ trace length with 100 mA current through 1 oz copper at 35°C, I want to keep the voltage drop to less than 10 mV. This requires the trace resistance to be less than 100 $\Omega$ . Under these conditions, no more than 1 mW power will be dissipated in this trace. This time though, I’ll allow a 5°C temperature change.

The resistivity of the copper will be:

$\begin{displaymath}\rho(T) \; = \; \left[ \, 606.64 \, + \, 2.684 \times (\, 35 \, + 5 \, ) \, \right] \; = \; 714.00 \; \mu \Omega \cdot \text{mil}\end{displaymath}$

and the minimum effective area is found to be 42.84 mil² which requires an internal trace to be at least 31.1 mils wide. An external trace would only need to be 15.5 mil wide. Quite a bit different than that calculated in the first example.

One more example should do it …
Again, 6″ of 1 oz copper at 35°C. My trace is now 60 mil wide and carries 200 mA. This gives an area of 165.4 mil².

The change in temperature is 0.12°C for an internal layer; insignificant for an external layer. Resistivity is 700.6 $\mu \Omega \cdot \text{mil}$ . The resistance is 25.4 m $\Omega$ (4.2 m $\Omega$ /in) with a total voltage drop of about 5.08 mV for either internal or external layer (about 0.85 mV/in). A squiggle over 1 mW will be dissipated.

An estimate for trace capacitance in pF could be expressed as:

$\begin{displaymath}C(pF) \; = \; 0.31 \, \frac{ct}{cw} \, + \, 0.23 \, (\, 1 \, - \, k \, ) \, log \left[ \, 1 \, + \, 2 \, \frac{cw}{th} \, + \, 2 \, cw \, + \, cw^{2/th^2} \, \right] \; \Rightarrow \; 0.75 \, pF\end{displaymath}$

Concepts to consider for critical measurement circuits.

Leave a Comment Cancel Reply