Rise Time & Bandwidth – Dave McGlone

Rise time is defined as the time for a waveform to transition from 10% of the final steady-state amplitude to 90% of that amplitude (fall time is defined the same way … only on the falling edge).

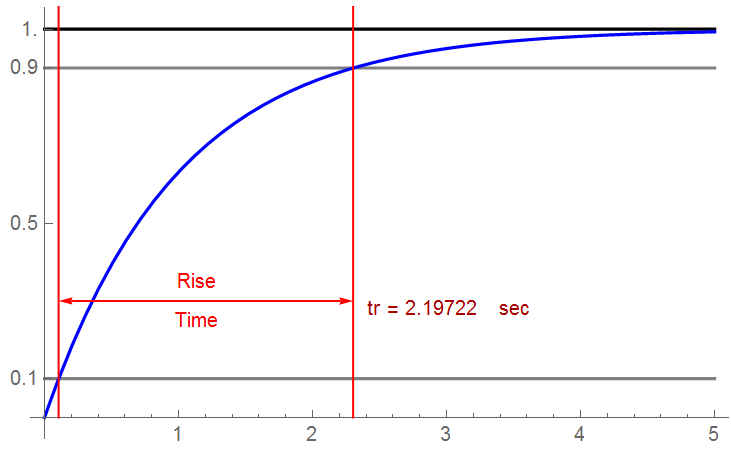
Calculating for a 1st-order response:

$\begin{displaymath}t \, = \, R \, C \: ln \left(\frac{V_{in}}{\, V_{in} - V_{out} \,} \right)\end{displaymath}$

$\begin{displaymath}t_r \, = \, R \, C \: ln \left(\frac{1}{\, 1 - 0.9 \,} \right) \, - \, R \, C \: ln \left(\frac{1}{\, 1 - 0.1 \,} \right)\end{displaymath}$

$\begin{displaymath}t_r \, = \, R \, C \: \left(\, 2.30259 - 0.10536 \, \right) \, = \, R \, C \: \left(\, 2.19722 \, \right)\end{displaymath}$

Define the low-pass bandwidth by the frequency where the amplitude has decreased by 3dB:

$\begin{displaymath}bandwidth \; = \; BW \; = \; f_{-3dB} \, = \, \dfrac{1}{ \, 2 \pi R C \,}\end{displaymath}$

For $\tau$ = R C:

$\begin{displaymath}t_r \, = \, \left(\, 2.19722 \, \right) \, \tau \quad \Rightarrow \quad \frac{t_r}{\, 2.19722 \,}\end{displaymath}$

$\begin{displaymath}BW \, = \, \frac{1}{\, 2 \pi R C \,} \quad \Rightarrow \quad { \, \frac{1}{2 \pi \frac{t_r}{\, 2.19722 \,}}\end{displaymath}$

$\begin{displaymath}BW \, = \, \frac{2.19722}{\, 2 \pi t_r \,} \quad \Rightarrow \quad { \, \frac{0.3497}{{t_r} \,}} \; = \; \frac{0.350}{t_r}\end{displaymath}$

So the minimum rise time needed to meet bandwidth requirements is found from:

$\begin{displaymath}t_r \; = \; \frac{0.350}{BW}\end{displaymath}$

And a minimum bandwidth of $\; \dfrac{0.350}{50e-9}\; = \;7$ MHz is required to maintain a rise time of 50 ns.

A handy little equation.

Why is this useful? All practical systems are ultimately limited by a reasonable approximation of a 1st-order low-pass filter – often the construction platform such as the PCB or IC process. As a rule-of-thumb, the system operating frequencies should be about 1 decade below the corner frequency when assuming 20 dB/dec attenuation (a voltage or current factor of 10).

If my system has a corner frequency of 1 GHz, the minimum theoretical and usable rise time would be 350 ps. Allowing a fudge-factor of 10, the minimum rise time would be 3.5 ns. This may have an effect on clocked systems, particularly when non-over-lapping clocks are incorporated in the design.

Kids Say the Darnedest Things

I’ve heard it stated by people that should know better that “rise time” only applies to 1st-order systems. Variations of the magnitude limits exist (although the 10% to 90% limits are standard for analog and digital electronic systems), the concept of rise time most definitely exists for 2nd-order (and higher) systems. The concept is particularly important in high-speed transmission systems.

In this 2nd-order illustration, the steady-state amplitude is 1.0, the rise time is 1.26 sec … and the ±5% settling time is 10.8 sec – but settling time’s a different topic (the CYN region defines ±5% limits)

That’s good for now.

Leave a Comment Cancel Reply