Sometime long ago I was asked to analyze a temperature sensing system which had an operating temperature of “about” 100K with a control limit of ±1mK. Stability of temperature is more important than the absolute value which is why I say “about 100K”.
The sensor excitation is rated at 10 mVmax; the sensor response time ranges from 0.25s at the lower end; 0.8s at the higher end. The project required a 1kHz bandwidth.
It is allowable that interface networks be in a warmer environment (>220K = -55°C) but that warmer environment is not temperature controlled.
The specific temperature sensor was defined. The “reproducibility” is rated ±3mK. I considered this to be a possible issue as this was the rating at the low end of the range (<50K); increasing as the temperature increases. The thermal responsivity is approximately a function of e-1.
The resistance variation needs to be extrapolated as the resistivity varies non-linearly from -15.4 Ω/K at 77K and -0.55 Ω/K at 300K.
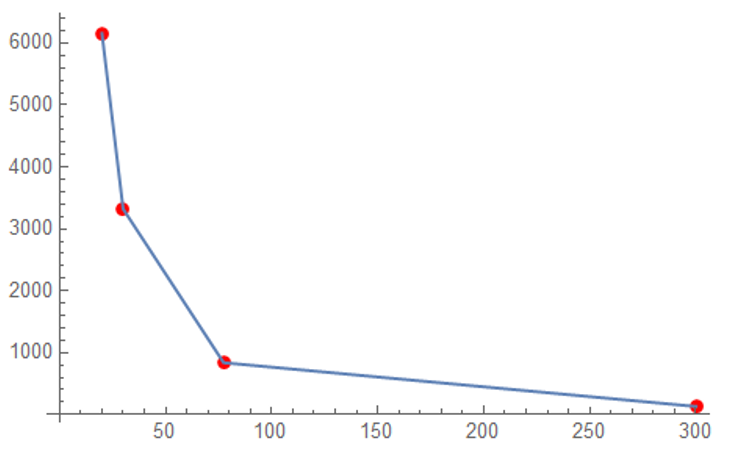
Only 4 performance data points are provided – from the given resistance vs temperature data; the given data are the 4 RED dots, I added the joining lines:
Applying a bit of curve-fitting using the following expression as a model:
![]()
I end up with a fit:

With the resulting coefficients:
- a = 3.8059e13
- b = 1.52681
- c = 7.60846e-6
- d = 42.5656
A similar examination of the derivative of resistance with respect to temperature (dR/dT) was undertaken with this result.

The desired temperature of operation is roughly 100K. A bit close to the inflection point but it’s possible the change of resistivity has stabilized at this temperature. The inflection point is at roughly 40K; this analysis is an estimate based on curve fitting – measurements should be made of the actual device.
This note was made in the report:
It appears these functions fit the available data. Noting the Response Data footnote: “the listed resistance ranges are typical, but can vary widely“, it will be assumed the following calculations are representative of the performance of a specific device and only suitable for initial design procedures.
Having been involved in designing spacecraft instrumentation off and on over several decades, low-temperature sensors have been of interest to me. My notes didn’t include the source for the following charts of available cryogenic temperature sensors.

The MAG lines indicate the 100K temperature and the resolution goal of 1 mK. The BLU arrows point out the characteristics of a platinum-based (Pt) detector.
None of the detector types – listed here – are capable of the desired performance. The CS-501 detector comes closest with Pt detectors close behind. The Pt sensor has the highest sensitivity at 100K.
Neither of these detectors is under consideration for this analysis.
The measurement network will essentially be an ohm-meter but I suspect my old Heathkit wouldn’t have been sufficient …
The sensor requires a constant excitation voltage. This implies that a measurement network be based on determining variations in current. Information was not available for change in resistance against change in excitation voltage (dR/dV).
A detailed examination of the resistance function for the desired detector over the narrow range of interest shows an essentially linear response.

The analytical slope of this function is -7.99307 mΩ/K … call it -8 mΩ/K. The nominal resistance at 100K is 566 Ω
A maximum excitation voltage of 10 mV suggest the detector current will be no more than 17.7 μA … maximum power dissipation within the detector being about 177 nW. Is this enough to be concerned about self-heating? The answer may be Yes but the related information was not available and such effect – if significant – would likely be no more than a stable offset. Since the absolute temperature is not an issue, self-heating is likely not an issue – power dissipation will be essentially constant to 1st-order.
Assuming a constant 10mV excitation, the current will vary by 498 nA over a temperature range between 99K and 101K. Assuming linearity, this implies a current change of 498 pA over a ±1 mK shift in temperature.
As of this writing – long after this analysis project took place – I can buy a battery operated fA/pA electrometer (Keysight B2980) for about  12K for room temperature measurements, not trivial.
12K for room temperature measurements, not trivial.
The cryogenic and physical environment suggest that excitation provided by a constant current source should be considered – with the change in voltage carrying the desired temperature information. The information needs to be contained within a voltage for the ADC anyway.
It was earlier determined that the maximum current allowed is just under 18 μA – consider a 15 μA constant current source for excitation.
The projected voltage change between 99K and 101K would be about 240 μV. Of course, the project requirements require stability to ±1 mK … which will create a voltage shift of 120 nV on top of a nominal common-mode voltage of about 8.5 mV.
To measure this voltage requires a resolution of about 0.0014% (-97dB). I suggest this is a bit tight … An idealized 16-bit converter has resolution of 0.00152% (96.3dB). An ideal 18-bit device would be suitable (108dB).
Of course, finding such a device to operate in the project environment may cause some consternation. Finding amplifiers with suitable CMRR at 1kHz could be difficult as well as considerations of hard-wire transmitting the signal from very, very cold to simply cold (100K to >220K) while maintaining signal accuracy. Noting the thermal time constants of the sensor, a reduction of required bandwidth to 10Hz would ease noise and CMRR issues.
The idealized rms voltage noise – assuming the required 1kHz bandwidth – can be calculated as 56 nV; the equivalent rms current noise would be 99 pA.
ADCs measure instantaneous values, not rms. Assuming a Gaussian distribution (perhaps not valid given the construction of the detector), the voltage noise would be 369 nVpp (without considering the amplification that would be required). This is significantly larger than the voltage change at 1 mK (120 nV).
The final conclusion? It is doubtful the project requirements as given can be met.
This was one of the projects that lead to “it’s not cynicism, it’s experience“. It wasn’t so much the sensor couldn’t meet requirements – it came close – it was the idea that the original requirements were kept and the word went uphill that the requirements would be met*. I did suggest the Pt-RTD be considered – at least to the level of comparing associated networks (I suspect the interface circuitry would have been less complex) – but the detector had already been committed to. Given the thermal response time of the detector itself, lowering the bandwidth to 10Hz would have provided a 10-fold improvement in theoretical noise – although I typically add 20% to the calculated noise value in the absence of empirical data.
*I think measuring to ±5 mK might have been possible – depending on the effort expended, the interface components, and the ADC, but ±100 mK would have been more practical. I didn’t then believe measurement resolution to ±1 mK would be feasible; it may not be now but I don’t have up-to-date information – possibly with a specialized IC. My task was complete with the analysis; I went on to other projects. My suspicion is that the issues with the thermal control – heating and control of the base plate – would likely have dictated the actual temperature variations.