Goal: Determine the effect on a function X(y) due to a change in parameter y. This is known as the sensitivity of X to y.
This is expressed:
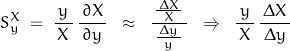
Consider a form of usage in Mathematica. Let X be “func”; let y be “m”. The expression equivalency is:
![]()
To implement in Mathematica:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}&\text{m = y;} \\&\text{func = X;} \\&\text{result} \; = \; \frac{\text{m}}{\, \text{func} \, } \, \text{D[func,m]}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-37b7c3cb5746b723896c958bb3595f39_l3.png)
An example … (Note: “![]() ” in Mathematica is the natural logarithm, aka “
” in Mathematica is the natural logarithm, aka “![]() “)
“)
First define the functions:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}&\text{func1 = x } \mathbb{e}^{\text{-y z } \, (\alpha \, + \, \Delta \alpha) } \\\\&\text{func2 = PowerExpand[Log[func1]] } \rightarrow \, \text{- y z }(\alpha \, + \, \Delta \alpha) \, + \, \text{Log[x]}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-5f6b1934171fd00298f07bf099acfc6c_l3.png)
Then define the expressions:
![]()
![]()
Consider a basic voltage divider.
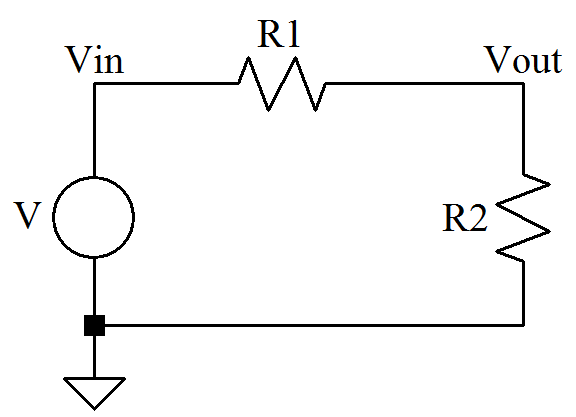
The transfer function of this network is:
![]()
The sensitivity of this function to changes in R![]() is:
is:
![]()
and for R![]() :
:
![]()
The sensitivities are identical except for the sign. The sensitivity of ![]() to changes in R
to changes in R![]() is negative: if R
is negative: if R![]() increases, the value of
increases, the value of ![]() decreases. However, the value of
decreases. However, the value of ![]() increases if R
increases if R![]() increases. If the two resistors are equal, the sensitivity is 0.5. This implies that a 1% change in either resistor will result in a 0.5% change in
increases. If the two resistors are equal, the sensitivity is 0.5. This implies that a 1% change in either resistor will result in a 0.5% change in ![]() .
.
In the limit, if R![]() >> R
>> R![]() , the sensitivity of
, the sensitivity of ![]() to changes in resistance tends to a value of 1; a 1% change in either resistor causes a 1% change in
to changes in resistance tends to a value of 1; a 1% change in either resistor causes a 1% change in ![]() . If R
. If R![]() >> R
>> R![]() , the sensitivity of
, the sensitivity of ![]() to changes in resistance tends to a value of 0; the function is essentially independent of changes in resistance.
to changes in resistance tends to a value of 0; the function is essentially independent of changes in resistance.
The most common variations in resistances are tolerance and temperature. Other possibly significant variations are voltage and load/life effects. Some applications will also require radiation tolerances … but those applications are quite specific – if you need them, you’ll know where and how to get them.
Voltage and aging coefficients are often ignored (and may not even be specified) but may have a significant effect in precision applications.
Some specifications for a precision resistor:
Tolerance: ±100 ppm (0.01%)
Temperature coefficient: ±0.2 ppm/C (-55°C to 125°C)
Power coefficient (self-heating): 5 ppm
voltage coefficient: < 0.1 ppm/V
load/life stability: 50 ppm (after 2000 hrs)
ESD: > 25 kV
thermal stabilization: ±10 ppm
rise time: 1 ns
Inductance: < 0.08 μH
A proper sensitivity analysis for a precision application will take each of these factors into consideration. The analysis of that simple resistor divider is no longer “simple” …
The same principles apply to reactive components and construction techniques as well (for example, flexing of a PCB can change the operational accuracy of a circuit. Many components will have flexibility criteria.)

That’s good for now.