Filtering – Part 2 – Dave McGlone

I left off with the suggestion that a higher order filter could be used to ease attenuation limitations on amplitude measurements, so let’s look at a 4th-order Butterworth response. The 4th-order filter could be constructed with two 2nd-order sections in cascade.

The normalized 2nd-order Butterworth function is:

$\begin{displaymath}T_{bw,2}(s) \; = \; \frac{1}{\, 1\, + \, s \, \sqrt{2} \, + s^2 \,}\end{displaymath}$

It follows that the 4th-order system constructed of two 2nd-order networks in cascade would be:

$\begin{displaymath}T_{bw,4}(s) \; = \; T_{bw,2}(s) \, \times \, T_{bw,2}(s) \; = \; \frac{1}{\, 1\, + \, s \, \sqrt{2} \, + s^2 \,} \: \times \: \frac{1}{\, 1\, + \, s \, \sqrt{2} \, + s^2 \,} \; = \; \frac{1}{\, 1\, + \, 2.82843 \, s \, + \, 4 \, s^2 \, + \, 2.82843 \, s^3 \, + \, s^4 \,}\end{displaymath}$

The magnitude response is:

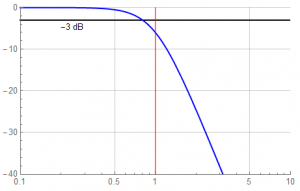
Wait a minute; that’s not right. The corner frequency is supposed to be “1”.

While two 2nd-order sections may be cascaded, the product won’t have the same coefficients as the 4th order filter will have.

The correct 4th-order function for a Butterworth response:

$\begin{displaymath}T_{bw,4}(s) \; = \; \frac{1}{\, 1\, + \, 2.6132 \, s \, + \, 3.41431 \, s^2 \, + \, 2.6132 \, s^3 \, + \, s^4 \,} \; = \; \frac{1}{\, 1\, + \, 0.7654 \, s \, + \, s^2 \,} \; \times \; \frac{1}{\, 1\, + \, 1.8478 \, s \, + \, s^2 \,}\end{displaymath}$

The component values for the filter are dictated by these polynomials but I don’t discuss filter design here …

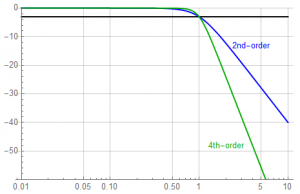
The point of this discussion is the magnitude response:

The 4th-order network has a steeper roll-off than the 2nd-order function … at the cost of a more complex network.

Let’s look at the passband in detail and see how that compares to the basic 2nd-order network. Both filters have a cut-off frequency of 1:

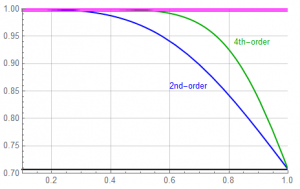
Again, the magenta lines represent the least-significant bits of 8, 12, and 16-bit conversion – the differences not really legible at this scale. It is obvious that the 4th-order filter has a “flatter” passband response to a higher frequency than the 2nd-order – at a cost of (moderately) increased circuit complexity and design effort.

Looking at the 12-bit and 16-bit limits, although there is significant improvement, the amplitude falls out of $LSB_{12}$ range at $\omega$ = 0.3856 and out of $LSB_{16}$ range at $\omega$ = 0.2726 … requiring the corner frequency to be about 3.5x greater than the highest signal frequency.

An 8th-order filter starts to become unreasonable except in special circumstances – it begins to enter the realm of diminishing returns and one should begin to question the overall network philosophy if such higher order filters are called for. The answer may justify their use, but the question should still be raised.

An 8th-order magnitude response with 2nd and 4th-order responses for comparison:

Looking at the passband:

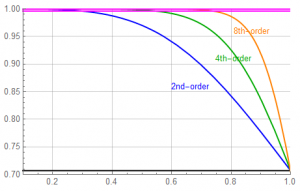
And, finally, a comparison of the 12 and 16-bit error bounds for the 8th-order Butterworth response.

While the 8th-order filter significantly eases requirements on the sample frequency over that of the 2nd-order, the added complexity suggests a different approach may be justified.

Part 1
Part 3

More issues to come but
That’s good for now …