It’s time to consider the transient and frequency response of this network:
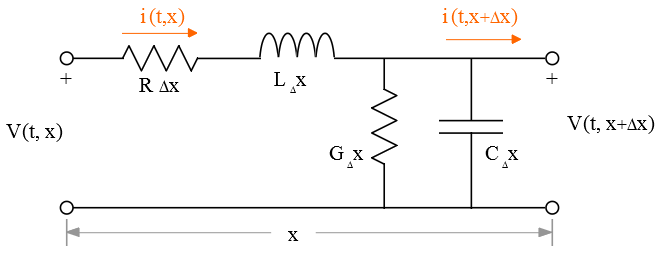
The transform voltage along the line in terms of the transform voltage at the input is given as:
![]()
Apply a unit-step impulse where Vo(s) = s-1
![]()
The only singularities are the poles of V(s,x) which are located at s = 0. The roots of sinh(Γd) = 0 come from:
![]()
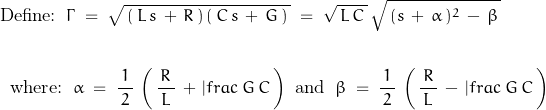
Combining equations gives:
![]()
The poles are complex for large k, may be negative real for small k
Generalizing the pole locations:
![]()
The inverse Laplace Transform is found using the residue theorem.
For t > 0:
![]()
which leads to:
![Rendered by QuickLaTeX.com \begin{displaymath}v(t,x)\;=\;\left[\,\frac{\,\mathit{sinh}\Gamma\,(d-x)\,}{s\,\mathit{sinh}\Gamma d}\,\mathit{e}^{st}\,\right]_{s=0}\;+\;\sum_{k=1}^\infty\,\left[\,\frac{\,\mathit{sinh}\Gamma\,(d-x)\,}{s\,\dfrac{d}{d s}\left(\mathit{sinh}\Gamma d\,\right)\,}\,\mathit{e}^{st}\,\right]_{s=-\alpha\pm\mathit{j}\omega_k}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-9f629a8222605a06cd4c47ceabed1b35_l3.png)
At s = 0, ![]()
At s = -α + j ωk:
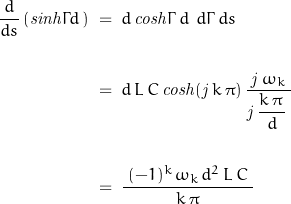
From ![]()
![Rendered by QuickLaTeX.com \begin{displaymath}\left[\,\frac{\,\mathit{sinh}\Gamma\,(d-x)\,}{s\,\dfrac{d}{d s}\left(\mathit{sinh}\Gamma d\,\right)\,}\,\mathit{e}^{st}\,\right]_{s=-\alpha\pm\mathit{j}\omega_k}\;\;=\;\;\frac{k\,\pi\,\left(\,\dfrac{\,k\,\pi\,x\,}{d}\,\right)}{\,d^2\,L\,C\,\omega_k\,\sqrt{\,\omega_k\,+\alpha\,}\,}\,\mathit{e}^{-\mathit{j}\,\Theta}\qquad \textnormal{where:}\;\;\Theta \,=\;\mathit{tan}^{-1}\frac{\alpha}{\,\omega_k\,}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-d887df531418a3d41aa83791a8ab4b73_l3.png)
Finally coming to the solution:
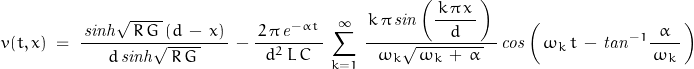
The first term is the steady-state solution; the second is the transient solution.
If the line is a lossless LC network; i.e., R = G = 0
![]()
giving the solution:
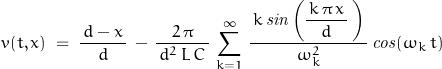
Now consider a distributed RC network; i.e., L = G = 0 stimulated by a unit-step input. Although the above derivation may be used, consider the following:
The transform of the voltage across the network as a function of position is given as:
![]()
With a unit-step input:
![]()
Noting ![]()
the roots are located at ![]()
A bit of algebraic tweaking gives:
![]()
That’s good for now. Next: Lumped Parameter Representation
