Distributed Parameters 3 – Non-Uniform Distribution

The transmission lines are not always uniform across the line. Assume the following network:

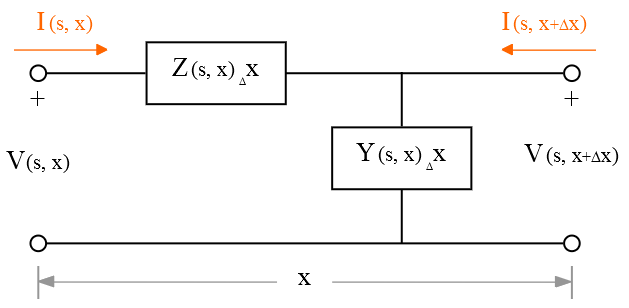
Both the per-unit-length series impedance and shunt admittance are functions of s as well as x. We assume initial conditions are zero: no magnetic flux in inductances, no charge on capacitors. The equations based on incremental models assume a single-dimension variation.

$\begin{displaymath}\begin{align}\frac{\,d V(s,x)\,}{d x}\;&=\;-Z(s,x)\,I(s,x)\\\\\frac{\,d I(s,x)\,}{d x}\;&=\;-Y(s,x)\,V(s,x)\end{align}\end{displaymath}$

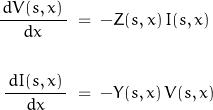
Differentiating

$\begin{displaymath}\begin{align}\frac{\,d^2 V(s,x)\,}{d x^2}\;&=\;-Z(s,x)\,\frac{\,d I(s,x)\,}{d x}\,-\,I(s,x)\,\frac{\,d Z(s,x)\,}{d x}\\\\\frac{\,d^2 I(s,x)\,}{d x^2}\;&=\;-Y(s,x)\,\frac{\,d V(s,x)\,}{d x}\,-\,V(s,x)\,\frac{\,d Y(s,x)\,}{d x}\end{align}\end{displaymath}$

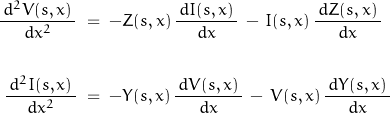
Tweaking these results a bit provides a pair of equations relating the voltage and current to any point x

$\begin{displaymath}\begin{align}\frac{\,d^2 V(s,x)\,}{d x^2}\;&=\;-\left[\,\frac{1}{\,Z(s,x)\,}\,\frac{\,d Z(s,x)\,}{d x}\,\right]\,\frac{\,d V(s,x)\,}{d x}\,-\,Y(s,x)\,Z(s,x)\,V(s,x)\;=\;0\\\\\frac{\,d^2 I(s,x)\,}{d x^2}\;&=\;-\left[\,\frac{1}{\,Y(s,x)\,}\,\frac{\,d Y(s,x)\,}{d x}\,\right]\,\frac{\,d I(s,x)\,}{d x}\,-\,Y(s,x)\,Z(s,x)\,I(s,x)\;=\;0\end{align}\end{displaymath}$

Set Z(s,x) = Z(s) F₁(x) and Y(s,x) = Y(s) F₂(x) where Z(s) = R(x) + s L(s) and Y(s) = G(s) + s C(s)

$\begin{displaymath}\frac{\,d^2 V(s,x)\,}{d x^2}\;&=\;-\left[\,\frac{1}{\,F_1(x)\,}\,\frac{\,d F_1(x)\,}{d x}\,\right]\,\frac{\,d V(s,x)\,}{d x}\,-\,Y(s)\,F_1(x)\,\,Z(s)\,F_2(x)\,V(s)\;=\;0\end{displaymath}$

The solution to this expression can be in the form of V(s,x) = a V_a(s,x) + b V_b(s,x)

$\begin{displaymath}\textnormal{Since}\;\;I(s,x)\;=\;-\frac{1}{\,Z(s,x)\,}\,\frac{\,d V(s,x)\,}{d x}\end{displaymath}$

$\begin{displaymath}I(s,x)\;=\;-\frac{1}{\,Z(s,x)\,}\,\left[\,a\,\frac{\,d V_a(s,x)\,}{d x}\,+\,b\,\frac{\,d V_b(s,x)\,}{d x}\,\right]\end{displaymath}$

$\begin{displaymath}\begin{align}\textnormal{From:}\;\;\frac{\,d^2 V(s,x)\,}{d x^2}\;&=\;-\left[\,\frac{1}{\,F_1(x)\,}\,\frac{\,d F_1(x)\,}{d x}\,\right]\,\frac{\,d V(s,x)\,}{d x}\,-\,Y(s)\,F_1(x)\,\,Z(s)\,F_2(x)\,V(s)\;=\;0\\\\\frac{\,d^2 V\,}{d x^2}\;&=\;-\left[\,\frac{1}{\,Z\,}\,\frac{\,d Z\,}{d x}\,\right]\,\frac{\,d V\,}{d x}\,-\,Y\,\,Z\,V\;=\;0\\\\\textnormal{or}\;\;&V"\,-\,\frac{\,Z'\,}{Z}\,V'\,-\,Y\,Z\,V\;=\;0\end{align}\end{displaymath}$

That’s good for now. Next: General 2-Port

Leave a Comment Cancel Reply