The determination of non-uniform current flow and equipotential lines of force are aided by the use of other coordinate systems. There are four coordinate systems feasible for 2-d networks: rectangular (Cartesian), polar, parabolic, and elliptic. Expressions are developed for the polar and parabolic systems.
Polar
Consider a polar coordinate system. This geometry represents a linear electrical taper.
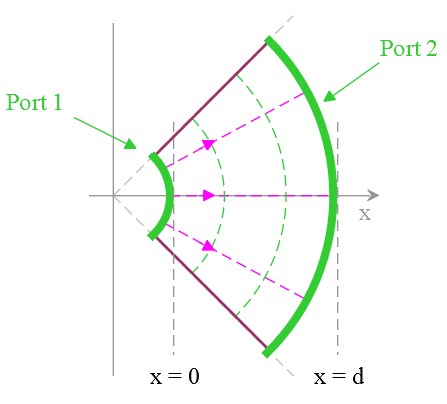
In this system, equipotential lines are circles; current flow follows radii. Port 1 will be defined as x = 0; port 2 is at x = d. The coordinate system center is at x = – x0. The network width is found from:
![]()
where ![]() is the network width at x = 0 and
is the network width at x = 0 and ![]() is the angle of the network.
is the angle of the network.
Capacitance is measured per-unit-length as measured radially and is proportional to width; resistance per-unit-length is inversely proportional to width.

where c0 and r0 are the capacitance and resistance at x = 0
Computing the voltage at various points in the network where voltage V0 is at port 1 and zero voltage at port 2. The pertinent expression is
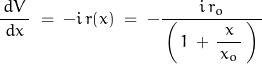
where ![]()
The network resistance is found from
![]()
From Ohm’s Law:
![Rendered by QuickLaTeX.com \begin{displaymath}V(x)\;=\;V_o\,\left[\,1\,-\,\dfrac{\,\mathit{ln}\left(\,1\,+\,\dfrac{x}{\,x_o\,}\,\right)\,}{\,\mathit{ln}\left(\,1\,+\,\dfrac{d}{\,x_o\,}\,\right)\,}\,\right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-e08c156aec886a230df89d9469671491_l3.png)
The voltage drops are not linear with length; the point where the potential is V/2 occurs where
![Rendered by QuickLaTeX.com \begin{displaymath}2\,\mathit{ln}\left(\,1\,+\,\dfrac{x}{\,x_o\,}\,\right)\;=\;\mathit{ln}\left(\,1\,+\,\dfrac{d}{\,x_o\,}\,\right)\;\;\textnormal{where}\;\;x\;=\;x_o\,\left[\,\sqrt{\,1\,+\,\dfrac{d}{\,x_o\,}\,}\,-\,1\,\right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-c5c47659ccee04dca4a6f2b2de966a81_l3.png)
Parabolic
A network on a parabolic coordinate is illustrated. Equipotential lines are in GRN; constant current lines are in MAG. A network laid out on a parabolic coordinates approximates a square root electrical taper.

The coordinates of this system are P and Q where lines of constant P (equipotential) fit:
![]()
and lines of constant current Q
![]()
Referring to the figure, Port 1 is selected such that P = C0; Port 2 is at P = C4. Q is orthogonal to P and the boundary will be Q = ±K
The potential V is determined by applying separation of variables where ![]() . F and G must satisfy:
. F and G must satisfy:
![]()
To determine r(x) and c(x), the network width along equipotential lines of P must be defined.
x = ½ (D2 – Q2) and y = D Q so that:
![]()
The network width along an arc length is found by integrating
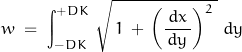
where y = DQ and the network is bounded by ±K
After a bit of tweaking
![Rendered by QuickLaTeX.com \begin{displaymath}w(x)\;=\;K\,\left(\,1\,+\,\sqrt\,2\,x\,+\,k^2\;}\,\right)\,+\,\frac{\,2\,x\,+\,k^2\,}{2}\,\mathit{ln}\,\left[\,\frac{\;K\,+\,\sqrt{\,2\,x\,+\,k^2\;}\,}{\;K\,-\,\sqrt{\,2\,x\,+\,k^2\;}\,}\,\right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-1e0112448544cd4d95ede25ad542ce4f_l3.png)
Other methods may be considered but are not discussed here (hasn’t this been enough?)
Design Example: LP Filter
A single stage low-pass filter transfer function is given as
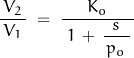
For a uniformly distributed RC network, the transfer function is modified to
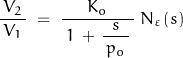
where Nε contains the error poles and zeroes of the network.
Assume the filter is to have a magnitude error of less than 1 dB and a phase error not to exceed 10° from DC to 10 ωo. Nε is now constrained to
![]()
At this point, the expression Nε for has not been determined.
The desired structure is of the form:
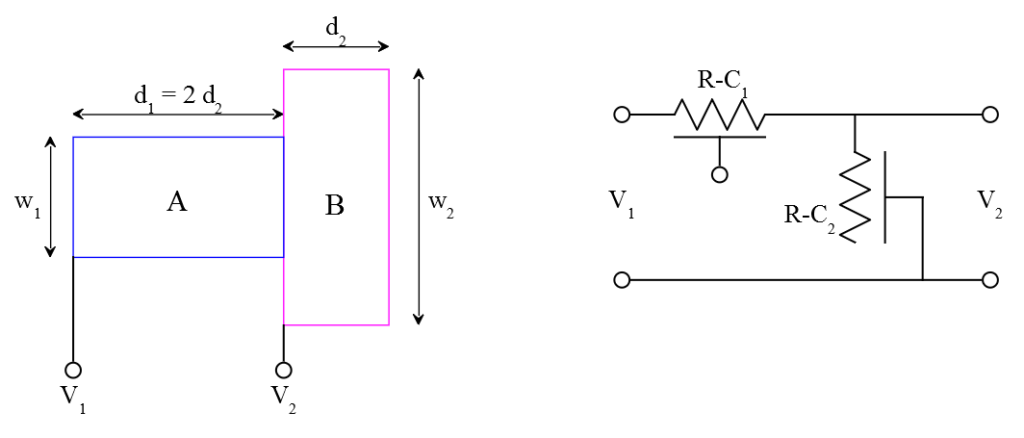
There are two distributed RC networks in which one has twice the dimension d as the other. This network has a transfer function of:
![]()
where ![]() and with poles located at
and with poles located at
![]()
The secondary poles are located in pairs at approximately ![]()
If ![]() is large and
is large and ![]()
(if K = 10, then k = 0.43; if K = 100, then k = 0.14)
If k << 1, Nε is approximately
![Rendered by QuickLaTeX.com \begin{displaymath}N_\varepsilon\;\approx\;\prod_{n=1}^\infty\,\left[\,\dfrac{1}{\,1\,+\,\dfrac{s\,T_B}{\,(\,n\,\pi\,)^2\;}\,}\,\right]^2\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-7a964f398e25f54efd7a4e35c791ac85_l3.png)
Expanding the magnitude of this expression:
![]()
Applying the network constraints: ![]() and
and ![]()
giving ![]()
With the 2nd dominant pole located at ![]()
![]()
The phase of the error function Nε is ![]()
If ![]() , the tan-1 coefficient may be replaced with its angle such that
, the tan-1 coefficient may be replaced with its angle such that
![]()
At ![]()
![]()
From the magnitude requirements, the 1st pole must be 43 times further from the origin than po. The phase restriction requires that p1 be 188 times further than po
Solving for K
![]()
Consider: Is the initial approximation assumption for ![]() still valid?
still valid?
The lumped RC network now provides the desired transfer function
![]()
Note that loading the network tends to reduce the separation of dominant and non-dominant poles in which case a larger value of K is necessary
And that’s a wrap. Been fun, eh? Back to Articles page
