The Fourier Series for a finite sum may be defined as:
![Rendered by QuickLaTeX.com \begin{displaymath}\mathbb{F}_n(x) \; = \; a_o \, + \, \sum_{n=1}^N \left[\, A_n \, \text{cos}(nx) \, + \, B_n \, \text{sin}(nx) \, \right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-c1ebe1cf94b260ef8c9a08ace966cf0b_l3.png)
where
The coefficients are found to be:
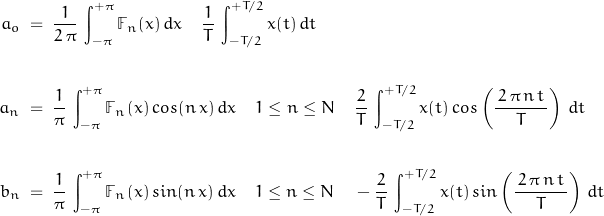
For an amplitude-offset square wave, the function may be defined:
![Rendered by QuickLaTeX.com \begin{displaymath}\[ f(x) = \left\{ \begin{array}{ll}0 & \mbox{if $-\pi \leq x < 0$};\\\pi & \mbox{if $0 \leq x \leq \pi$}.\end{array} \right. \]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-e4bf7e03c5fe0f5d3b9bd94b1e33f835_l3.png)
where
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}a_o \; &= \; \frac{1}{2 \, \pi} \, \left( \, \int_{-\pi}^0 0 \, dx \, + \, \int_0^\pi 0 \, dx \, \right) \; = \; \frac{\pi}{2} \\\\a_n \; &= \; \int_0^\pi \pi \, cos(n \, x) \, dx \; = \; 0 \quad n \geq 1 \\\\b_n \; &= \; \int_0^\pi \pi \, sin(n \, x) \, dx \; = \; \frac{1}{n} \, \left[ \, 1 \, - \, cos(n \pi) \, \right] \; = \; \frac{1}{n} \, \left[ \, 1 \, - \, (-1)^n \, \right]\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-c563e9bd687cb31f637882c8b7312755_l3.png)
where
![]()
which gives:

Consider a pulse sequence of amplitude A and duty-cycle d (where d = k/T) centered about 0. By definition, this is an even function:
![Rendered by QuickLaTeX.com \begin{displaymath}\[ x(t) = \left\{ \begin{array}{ll}A & \mbox{for $-k/2 \leq t \leq k/2$};\\0 & \mbox{elsewhere}.\end{array} \right. \]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-9a93e227f348b076d4bdf06060855ee7_l3.png)
The even-function coefficients are found from:
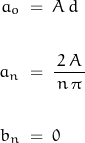
If ![]() and
and ![]() , then the amplitudes for the first several terms are:
, then the amplitudes for the first several terms are:

Put into Mathematica code:

Gives this result:
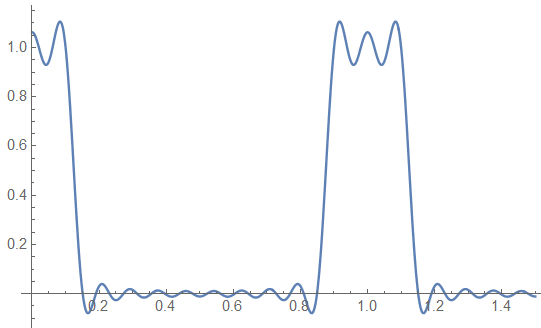
The Gibbs Effect “ears” are prominent and indicate about 9% over and under shoot.
But the function is even – centered about 0; the full response appears as:
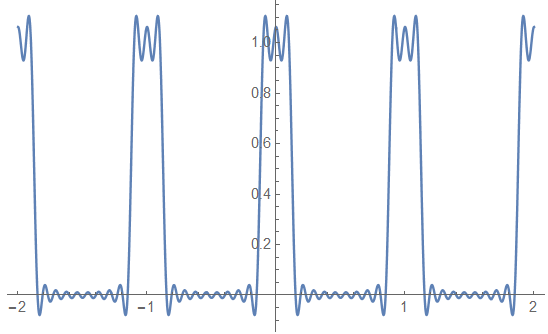
… sort of “sloppy” with only 13 terms (with DC).
If I calculate for 1200 terms, I get this:
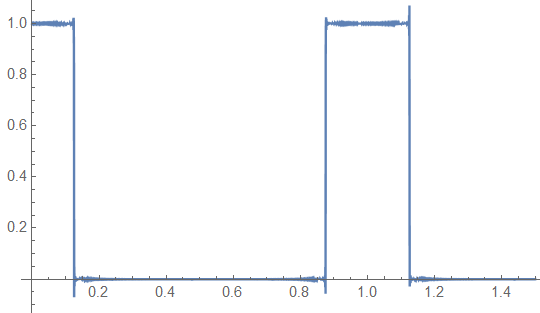
The Gibbs “ears” remain at about ![]() 9%, but the duration decreases as N increases and the energy content tends to 0.
9%, but the duration decreases as N increases and the energy content tends to 0.
Time-shifting the function will alter the coefficients (Coefficients ![]() are only zero if the function is centered about 0; i.e., an even function).
are only zero if the function is centered about 0; i.e., an even function).