Atmospheric CO2b – C Circuit Signal Attenuation

Signal Attenuation From CO2

CO₂ is a ubiquitous atmospheric gas. A certain portion of the on-wavelength signal will always be absorbed. The interest is in measuring any change in that absorption… so the on-wavelength signal is compared to a slightly off-wavelength signal. The system is configured such that “100% spatial and temporal overlap [1]” occurs. This eliminates sensitivity to “highly varying surface reflectance as well as minimizing effects of atmospheric turbulence by making it common-mode.[2]” (Note to me: this advantage is thrown away by the selected processing method)

I have been informed that a gross approximation of received signal strength is to assume about a 60% loss of signal. Using that value as a starting point, I can make the following declaration for “nominal” conditions:

Setting z to the approximate flight altitude of perhaps 30,000 ft (9.1km) and rounding up to 10km, I can calculate a value for parameter a of  0.04581 units/m over a path length of 20 km

My 1^st-order model will be of a cylindrical beam of uniform diameter. Define axes x,y as normal to the beam; z is coincident with the beam. If I assume uniform axial properties, I can analyze this model in the limit of a zero-diameter ray path. Using piece-wise linear approximations, I configure a three-layer system with step-junctions.

I configure the model to represent a “cloud” of anomalous CO₂ concentration with upper and lower regions of “nominal” concentration. With this model, the specific absorption numbers are irrelevant; I’ve defined the nominal CO₂ concentration (about 390ppm/m³) as a factor in the definition of a. Therefore, I can continue this analysis with relative values of abnormal concentration levels.

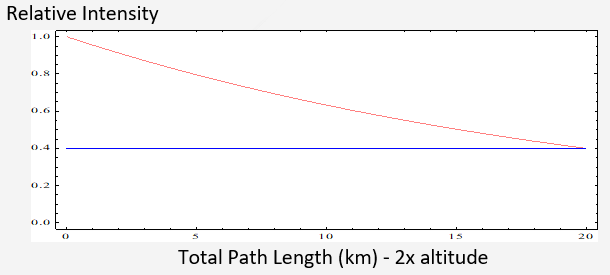
The basic beam intensity plot vs. path length is shown below: The RED is the beam intensity; the BLU is relative nominal concentration level at receiver.

The transmit intensity is normalized to 1. For the time being, I assume perfect reflection from a normal surface. I only consider amplitude … because that’s what’s measured with the photodetector.

The issue comes up: intensity of beam is directly related to numbers of photons generated by the laser. A certain portion of those photons strike the photo-detector and are converted to electron-hole pairs. Number-of-photons is not measured: a hopefully linear mapping of number-of-photons to electron-hole pairs to current is mapped – the amplitude of the current out of the photodiode is the actual measurement.

The model is developed to emphasize macro changes in the reflecting surface and the dual-path travel through the anomalous layer. Follows is an illustration of the model output under nominal conditions

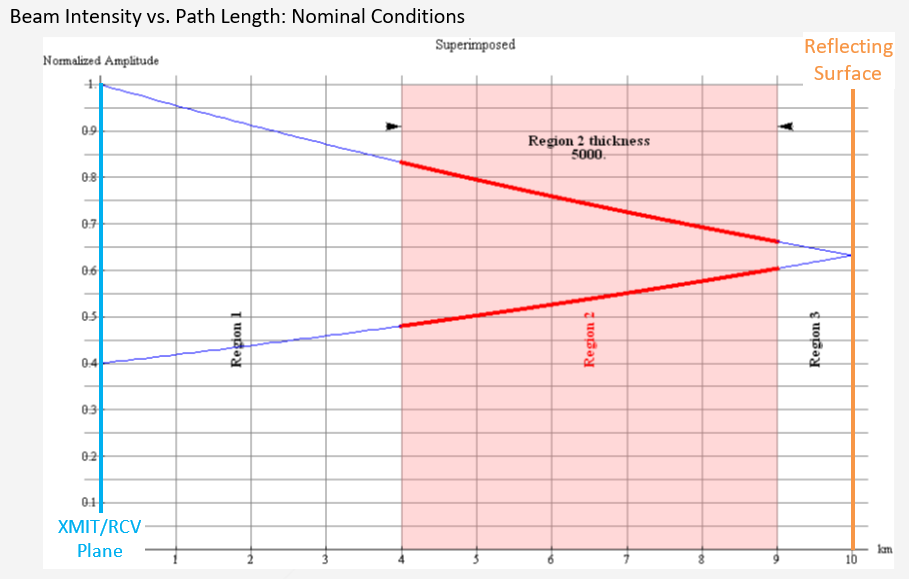
The left hand boundary represents a reflecting surface – presumed to be the Earth surface. The right hand boundary represents the transmit and receive instruments. I assume the laser and photodiode are collinear enough to not matter.

The anomalous layer is in PINK. In this case, an anomalous region has been defined as 5km thick at 1km above the reflecting surface. The BLU represents the intensity through the nominal regions. The RED shows the intensity variation due to a change in concentration. The intensities are identical in this illustration. The next illustration shows a grossly exaggerated variation in concentration.

To demonstrate the model flexibility, I have adjusted the anomalous layer to be 7km thick at 2km above ground level. There is a 60% increase in CO₂. The GRN path shows the intensity without the anomalous concentration.

This illustration is constructed as a visual and calculation aid. The signal information is contained within the amplitude of the intensity at the photodetector.

The expression to calculate the magnitude of the received signal is:

where So is the transmitted power (normalized to a value of 1); RC is the surface reflection coefficient (also normalized to 1); zmax is the height above the reflecting surface; are the normalized concentrations of CO2, z12 is the distance between the laser and the upper anomalous layer; and z23 is the distance between the bottom of the anomalous layer and the reflecting surface.

A few representative values have been calculated and presented in the following table to give an idea of the resolution required of the receiving network.

A full representation would require a multi-dimensional analysis including variations in layer thickness and concentration; it being assumed that factors such as ground reflectivity (including both angle and material variations) and scattering are nullified by the reference channel.

Example Number	Layer Thickness (km)	Relative Concentration	Reflection Angle	Relative Intensity
1	10	1.001	90	0.399641	0.359E-3
2	10	1.01	90	0.396424	3.576E-3
3	10	1.1	90	0.365647	34.350E-3
4	1	1.1	90	0.396352	3.648E-3
5	1	1.1	89	0.396110	3.890E-3

However, I need to note that reflectivity, etc affect the common-mode signal range and do justify consideration when defining the absolute range of intensity levels striking the photodiode  (Keep in mind that although the differential measurements represent the change in intensity due to CO2 concentration, the common-mode variations in intensity will limit the absolute detection range).

Note the difference between examples 2 and 4: How can one reasonably differentiate between a narrow region of high concentration (Example 4) and a thicker region of lesser concentration (Example 2)?

In an ideal sense, the reflectivity variations between Examples 4 and 5 would be extracted by the differential nature of the measurement assuming the intensity change remained within the acceptable common-mode range of the instrument.

The brief discussion of sensitivity indicated an equal function sensitivity to length and concentration when determined as percentages. In order to achieve concentration measurements to “1ppm per volume” the resolution of altitude should be considerably better than this – which works out to an equivalent percentage of 1ppm/380ppm or 0.26%. This requires altitude knowledge within about ±37.5ft of a 30,000 ft altitude.

With that altitude error, the variation in signal cannot be distinguished between CO₂ concentration and altitude variation. Standard testing criteria would require the altitude be known to within ±3.75ft (10x better than measurement resolution) to claim a phenomena measurement of 0.26%. The flight data for the proposed aircraft indicates an altitude tolerance of about ±15ft. This suggests a measurement accuracy of about 2.5% or 10ppm/m³

To put another way, altitude accuracy appears to be the limiting factor in measurement resolution.

I proceed by assuming exact and constant path length – keeping in mind this is a highly idealistic model with the intent of reducing “over-engineering” rather than correcting “under-engineering” (a similar analysis with different parameters).

---

[1] Browell, ibid

[2] ibid

Next: TBD