Density is a measure of the number of particles per volume. Recall that one form of the Beer-Lambert defines attenuation constant as the product of absorption or scattering cross-section of each particle and the number of particles per volume … particle density.
A uniform particle distribution can not be assumed along a vertical atmospheric optical column, particularly in scattering elements. Atmospheric pressure/density is of concern in the determination of number of attenuation/absorption elements within the optical volume.
The particle density varies with temperature, pressure, and altitude. This is true with scattering particles as well as absorption particles.
The optical depth expression may also be expressed in terms of density as:
![]()
in which describes the opacity of the material and is the material density.
Particle density is not temperature insensitive.
The absorption probability is generally much higher closer to the reflecting surface (assumed a perfectly reflecting Earth).
Ideal Gas Relationship
Density may be determined from the ideal gas relationship PV = nRT
From this, volume is found:
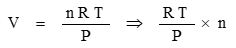
The number of mols of a gas is found from the ratio of the sample mass to the chemical molar mass:
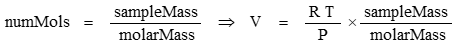
Density is mass/volume
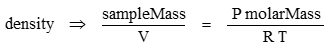
The molar mass of CO2 is 44.01 g/mol. R is the gas constant with a value of 8.31446 J m-1 K-1. Pressure P has units of kg m-1 s-2 → Pa
Checking units …
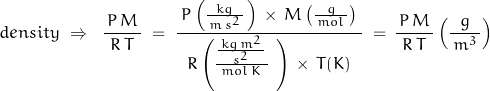
The ideal gas law states a relationship between pressure and density:
![]()
where P is pressure, ![]() is density, R is the gas constant, and T is temperature in Kelvin.
is density, R is the gas constant, and T is temperature in Kelvin.
The value for the gas constant is related to the gas of interest such that:
![]()
where Rc [1] is the universal gas constant and mW is the molecular weight (molar mass) of the gas.
The ideal gas law could also be expressed
![]()
The gas constant for a dry atmosphere at sea level would be calculated as
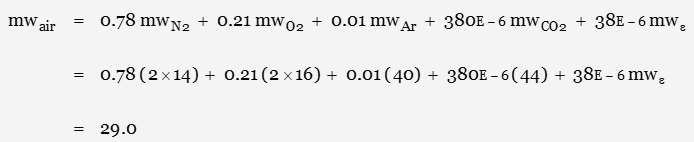
where mwe represents “everything else”: a mixture of all the other gases (except water vapour) in the atmosphere. At such a low percentage, the contribution is considered insignificant.
[1] per NIST: Rc = 8314.3 J K-1 kg-1
Atmospheric models
Ideal Gas
The ideal gas expression is:
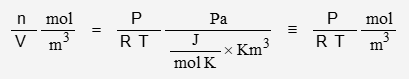
P is pressure, R is the gas constant, T is temperature, V is volume, and n is quantity. n/V is density in mol/m3. To convert to number of molecules, multiply by Avogadro’s Number:
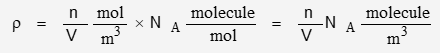
The nominal concentration of CO2 is 400 ppmv. The molar mass of CO2 is 44.01 g/mol
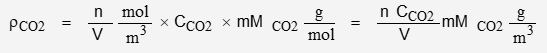
Using the appropriate values for the physical constants:
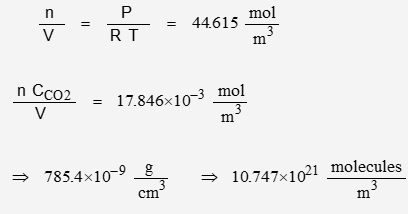
The volume of a mol of ideal gas is a physical constant wherein V = 0.22414 m3/mol. The nominal CO2 concentration is given in units of “per volume”, therefore the volume fraction of CO2 is:
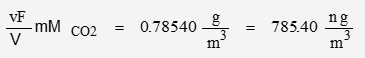
It will be convenient to define density in terms of molecules per volume:
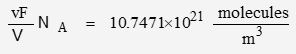
Dry Air
The assumptions required to use the ideal gas representation get stretched pretty far in the real world. A basic model could be based on the actual but idealized constituents of the atmosphere.
Using “dry air” parameters
massDensity = 1.2041 kg/m3
molarMass = 28.9644e-3 kg/mol
The molecular density of CO2 is found to be:
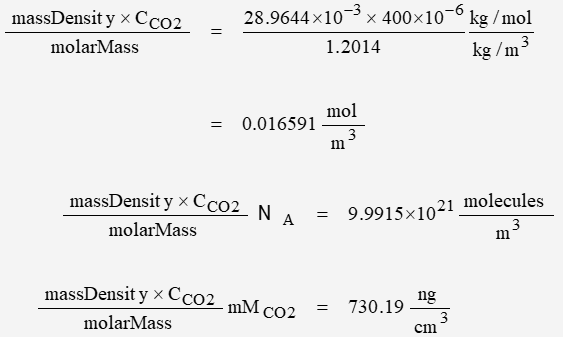
Standard Atmosphere
Yet another basic model is based on “standard” parameters. The parameters for the troposphere were defined in 1962; they were reviewed but not changed in 1976 for atmosphere below 32km. The intended altitude for this analysis is 10 km.
The air is clean, dry, and of uniform density. The molecular weight is 28.9664 g/mol
Sea-level values:
mWatm = 28.9664 g/mol
Patm = 101325 Pa
Tatm = 288.15 K
ratm = 1.2250 kg/m3
gatm = 9.80665 m/s2
Ratm = 8.3143 J mol-1 K-1
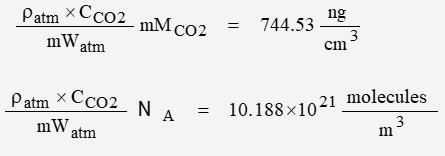
Comparing basic atmosphere models:
| Model | 1021 molecules/m3 | ng/cm3 |
| ideal | 10.7417 | 785.40 |
| dry | 9.9915 | 730.19 |
| stdAtm | 10.1878 | 744.53 |
| AVG | 10.307 | 753.37 |
Barometric Pressure and Temperature
The previous calculations were for sea-level conditions – recall that density is defined as:
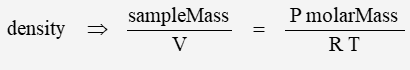
and is dependent on both pressure and temperature – which in turn vary with altitude.
Density is a function of pressure and temperature.
Representative empirical measurements: Spring 30oN
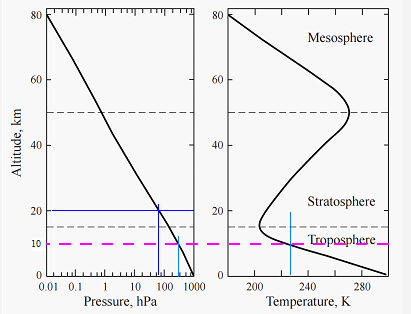
The MAG line represents the 10 km maximum altitude of interest. This is close to the boundary of the troposphere and stratosphere but far enough that tropospheric conditions remain valid for estimation purposes.
Temperature is essentially a linear function of altitude. From approximations derived from the above charts:
TCZ = -6.496 mK/m
A more detailed presentation of atmospheric density may be obtained from Density/Altitude information for aircraft. The Density-Altitude value expresses an effective altitude relative to a standard atmosphere. This is a function of temperature, pressure, and to a lesser degree, humidity. A hot and humid atmosphere may cause a density altitude higher than true altitude.
Density/Altitude Expression
An expression relating the three is given:
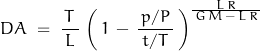
where:
P = 101.325 standard sea level pressure kPa
T = 288.15 standard sea level air temperature K
G = 9.80665 gravity
R = 8.31447 gas constant for ideal gas
M = 0.0289644 molar mass of dry air
L = 0.0065 lapse rate
Rdry = 287.058 J/(kg K) gas constant for dry air
RH2O =461.495 in J/(kg K) gas constant for water vapor
with p and t representing pressure and spot temperature.
Substituting values, the above expression reduces to
42023.1 [ 1 – 0.145317 (p/t)0.326034 ]
Humidity
Density is adjusted for humidity by the following … superposition principle
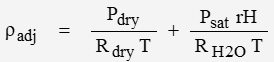
where rH is relative humidity and saturation pressure Psat can be estimated with:
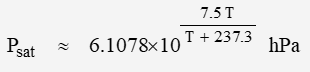
where units are hPa (equivalent to 1 mbar) and degrees C
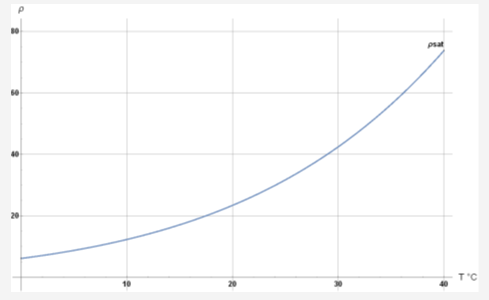
At a temperature of ~ 15C (288 K) and 50% relative humidity:
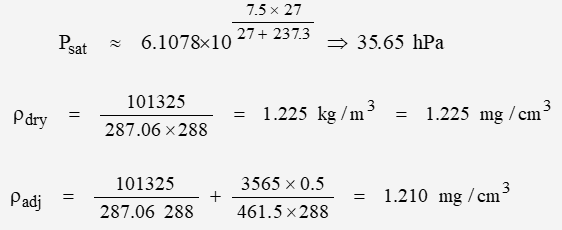
The barometric adjustment factor for pressure and temperature as functions of altitude:
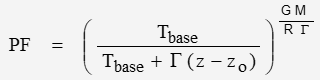
For sea-level, Pbase is atmospheric pressure of 101325 Pa and Tbase is sea-level temperature of 288.15 K. G is the lapse rate … in K/m
That’s all for now. Next 6: Atmospheric Carbon Dioxide
Back 4: Geometrical Construction
Up: Articles
