Atmospheric CO2 – Beer-Lambert & Optical Depth

Expression Development: Beer-Lambert Law*

Consider a section of optical path having length dz as shown below. The photon flux is considered uniformly distributed and cylindrical in nature. The flux is normal to the disk and the media is homogeneous.

A differential illustration of the optical path geometry is shown

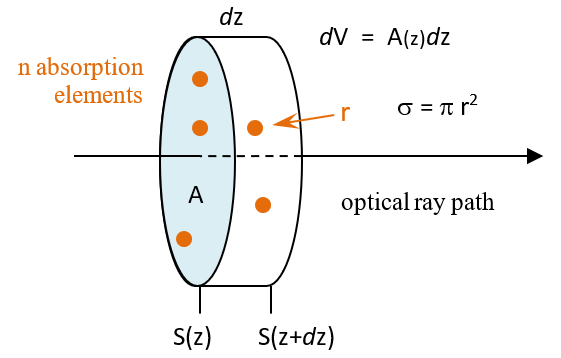
The cylinder has volume A $\times$ dz and contains n absorption elements, each of effective absorption radius r and having cross-section area $\sigma$ = $\pi$ r². The number of absorbers per unit volume is n $\times$ A $\times$ dz; the absorption cross-section is a function of species and energy level and a parameter of optical wavelength.

If the absorbers don’t shadow each other (true for dz → 0), the fractional area blocked is

$\sigma_{tot}\;=\;\sigma_a\,(\,n_a\,A\,dz\,)$

The amount of light blocked as a function of penetration distance is therefore

$\dfrac{\,\Delta\Phi\,}{\Phi}\;=\;\dfrac{\,\sigma_{tot}\,}{A}\;=\;n_a\,\sigma_a\,dz$

which follows the definition of optical depth: $\vartheta\;=\;n\,\sigma\,z$

The signal leaving the disk is simply the signal transmitted minus that portion absorbed (or scattered out of the path; not considered here).

If the optical depth is very small, the media is “thin” and the probability of interaction is also small. There are negligible amounts of absorption. (A fully transparent material has optical depth of zero.)

If the optical depth is very large, the media is “thick” and the probability of interaction resulting in scattering or absorption is very high.

However, an optically thick layer may be considered a sequence of optically thin layers.

Each thin layer has a change of intensity d $\Phi$ of the incoming intensity $\Phi$ multiplied by the optical depth of that layer such that

$\begin{displaymath}\begin{align}d\Phi\;&=\;-\Phi_o\,d n\,\sigma\,d z\;\;\Rightarrow\;\;-\Phi_o\,d \vartheta\\\\\frac{\,d\Phi\,}{\Phi_o}\;&=\;-d n\,\sigma\,d z\;=\;-d \vartheta\end{align}\end{displaymath}$

Integrating:

$\begin{displaymath}\begin{align}\int_{\Phi_o}^{\Phi_1}\,d\Phi\;&=\;-\int_0^\vartheta \,d \vartheta\;\;\Rightarrow\;\;\mathit{ln}\Phi\,\bigg|_{\Phi_o}^{\Phi_1}\;=\;-[\,\vartheta\,]_0^\vartheta\\\\&\Rightarrow\;\;\Phi\;=\;\Phi_o\,\mathit{e}^{-\vartheta}\\\\&\Rightarrow\;\;\mathit{ln}\left[\,\frac{\Phi}{\,\Phi_o\,}\,\right]\;=\;-n\,\sigma\,z\;=\;-\vartheta\end{align}\end{displaymath}$

The measured signal $\Phi$ is expressed

$\begin{displaymath}\begin{align}\frac{\Phi}{\,\Phi_o\,}\;=\;\mathit{e}^{-\vartheta}\;=\;\mathit{exp}\left[\,-n\,\sigma\,z\,\right]\\\\\Phi\;=\;\Phi_o\,\mathit{exp}\left[\,-n\,\sigma\,z\,\right]\;=\;\Phi_o\,\mathit{exp}\left[\,-\alpha\,z\,\right]\end{align}\end{displaymath}$

where $\alpha$ = n $\sigma$ ; the macro scale absorption cross-section

$\vartheta$ is a fractional quantity, the expression is unit-less and holds for any optical depth
(Note: about 50% transmission occurs for an optical depth of $\vartheta$ = 0.7)

*The Beer-Lambert Law is intended for short distances. Is it valid for long path lengths? I’ll assume the assumption.

Project-Specific OD Definition

The project has defined optical depth [1] as follows:

$\begin{displaymath}\vartheta\;=\;\int_0^Z\,K\,d z\;\;\Rightarrow\;\;N_{CO2}[cm^{-3}]\,\times\,\sigma_{CO2}[cm^2]\,\times\,z[cm]\end{displaymath}$

where Z is the total path length. N_CO2 describes the density of the specific gas (CO₂) of interest; $\sigma$ is the absorption cross-sectional area of CO₂ and assuming normal incidence upon the reflecting surface.

Units are such that N is number of CO₂ absorbers per unit volume; $\sigma$ is effective absorption cross-section area of the CO₂ absorbers, and Z is the optical path length (an implied 1-way path is inherent to the expression; the reflecting surface adds complexities to the system and is ignored for now).

The expression derived relates the received signal as a function of distance z to the initial signal at z = 0. Signal S is directly proportional to $\Phi$ .

$\begin{displaymath}\begin{align}S(z)\;=\;S(0)\,\mathit{exp}[\,-\vartheta\,]\;=\;&S(0)\,\mathit{exp}[\,-N_{CO2}\,\sigma_{CO2}\,z\,]\\\\\Rightarrow\;\;&S(0)\,\mathit{exp}[\,-n_a\,\sigma\,z\,]\\\\\mathit{ln}\left[\,\frac{\,S(z)\,}{S(0)}\,\right]\;=\;&N_{CO2}\,\sigma_{CO2}\,z\;=\;n_a\,\sigma\,z\end{align}\end{displaymath}$

such that the gas concentration in “number” per volume (m³) can be determined from

$N_{CO2}\;=\;\dfrac{1}{\,\sigma\,z\,}\,\mathit{ln}\left[\,\dfrac{\,S(z)\,}{S(0)}\,\right]$

where Z and S(0) are known [2], S(Z)is measured, and $\sigma$ is assumed known.

[1] Browell, et al, 2010, “Airborne Validation of LASER Remote Measurements of Atmospheric Carbon Dioxide”, EGU General Assembly 2010, Vienna, Austria – and related presentations

[2] distance z is actually measured but via a different process. The result is presumed a known quantity. A significant question is whether distance z is known to sufficient resolution.

Re-defining project terms for later clarity (assume all signals are functions of distance z):

$\begin{displaymath}\begin{array}{ l c l }Transmitted\, ON\, signal & S_{ON}(0) \,\rightarrow\, TX_{ON} & (Reference\, ON\, channel\, at\, z\, =\, 0\, ) \\Received\, ON\, signal & S_{ON}(Z) \,\rightarrow\, RX_{ON} & (Signal\, ON\, channel\, at\, z\, =\, Z\, ) \\Transmitted\, OFF\, signal & S_{OFF}(0) \,\rightarrow\, TX_{OFF} & (\,Reference\, OFF\, channel\, at\, z\, =\, 0\, )\\Received\, OFF\, signal & S_{OFF}(Z) \,\rightarrow\, RX_{OFF} & (\,Signal\, OFF\, channel\, at\, z\, =\, Z\, )\end{array}\end{displaymath}$

The differential measurement technique compares the absorption wavelength to the non-absorption wavelength such that

$\begin{displaymath}N_{CO2}\;=\;-\,\frac{1}{\,2\,H\,\sigma\,}\,\mathit{ln}\,\left[\,\frac{\dfrac{\;S_{ON}(z)\;}{S_{ON}(0)}}{\dfrac{\,S_{OFF}(z)\,}{S_{OFF}(0)}}\,\right]\;\;\equiv\;\;-\,\frac{1}{\,Z\,\sigma\,}\,\mathit{ln}\,\left[\,\frac{\dfrac{\,RX_{on}\,}{TX_{on}}}{\dfrac{\,RX_{off}\,}{RX_{off}}}\,\right]\end{displaymath}$

where H is the instrument platform altitude (Z = 2H). Z represents the total path length; $\sigma$ is the molecular absorption cross-sectional area; N_CO2 is the number of absorption molecules per unit volume. It is implied here that the reflecting surface is ideal.

A little tweaking gives:

$\begin{displaymath}\begin{align}\dfrac{\,RX_{on}\,}{TX_{on}}\;=\;&\dfrac{\,RX_{off}\,}{TX_{off}}\,\mathit{exp}\left[\,2\,H\,\sigma\,N_{CO2}\,\right]\\\\\equiv\;&\dfrac{\,RX_{on}\,}{RX_{off}}\;=\;\dfrac{\,TX_{on}\,}{TX_{off}}\,\mathit{exp}\left[\,2\,H\,\sigma\,N_{CO2}\,\right]\\\\N_{CO2}\;=\;&-\frac{1}{\,2\,H\,\sigma\,}\,\mathit{ln}\left[\,\dfrac{\,RX_{on}\,}{RX_{off}}\,\dfrac{\,TX_{on}\,}{TX_{off}}\,\right]\end{align}\end{displaymath}$

where RX_on/RX_off refer to the on-band and off-band measured signal; TX_on/TX_off refer to the on-band and off-band initial transmitted reference, and H is the altitude.

For defining initial parameters, assume the incident (reference) signals – TX_on and TX_off – are equal and constant (this implies both lasers are transmitting equal beam intensity which is likely not true in practice)

Assuming equal common-mode errors allows the ON/OFF signals to be defined as:

$\begin{displaymath}\begin{align}\frac{RX_{on}}{\,TX\,}\;&=\;\mathit{e}^{-z\,\alpha_{on}}\;\;\Rightarrow\;\;\mathit{e}^{-z\,(\,\alpha_a\,+\,\alpha_s\,)}\\\\\frac{RX_{off}}{\,TX\,}\;&=\;\mathit{e}^{-z\,\alpha_{off}}\;\;\Rightarrow\;\;\mathit{e}^{-z\,\alpha_s\,}\end{align}\end{displaymath}$

where absorption coefficient $\alpha_a$ = n $\sigma$

Other particles within the optical path – such as dust – will cause a loss of photons due to scattering rather than absorption (this is particularly true at the reflecting surface).

The photons lost to absorption are designated $\alpha_a$ while those lost to all other phenomena are designated $\alpha_s$ . It is implied that the ON channel will be attenuated more than the OFF channel.

The OFF-channel signal is designed such that it shares all errors with the ON-channel signal. Scattering, reflections, non-absorbance attenuation, multi-path reflections, ground reflections, etc are assumed common to both signals [1], [2].

The ratio of the ON signal to the OFF signal results in:

$\begin{displaymath}\frac{RX_{on}}{\,RX_{off}\,}\;&=\;\frac{\mathit{e}^{-z\,(\,\alpha_a\,+\,\alpha_s\,)}}{\mathit{e}^{-z\,\alpha_s}}\;\;\Rightarrow\;\;\frac{RX_{on}}{\,RX_{off}\,}\,\mathit{e}^{-z\,\alpha_a\,}\end{displaymath}$

Again, if S_OFF is normalized – allowing consideration of the relative change – the working expression is:

$RX_{on}\;=\;\mathit{e}^{-z\,\alpha_a}$

The common-mode scattering elements have no effect on the measurement (but they do partially define the necessary compliance range of the instrument)

[1] The spectral response is not discontinuous and is shaped more like a finger than a line. In actual implementation, the ON channel is slightly detuned from the “exact” species peak while the OFF channel is slightly within the response region. It is intended the differential difference be constant – as it is under the more ideal assumptions of this discussion

[2] The term “common-mode” refers to those elements shared by both signals. “Differential mode” refers to the differences between signals. It is the goal of this measurement to reject common-mode and extract differential-mode signal components.

Deviations From Beer-Lambert

The derivation illustrates the foundation for the basic expression of the Beer-Lambert Law. However, “shadowing” of particles along the path length, homogeneity of absorption elements, non-parallel ray paths, bi-directional ray paths, multiple absorption per absorber, and altitude-dependent particle density are among the significant deviations inherent to this project.

“Shadowing”: CO₂ molecules may “block” other CO₂ molecules – or absorb multiple photons.

Geometry:
The ray path is not sufficiently parallel: the cross-sectional area has significant deviation.
The optical paths are truncated cones rather than cylinders; the TX and RX paths are not identical.

Other present elements may have similar absorption characteristics: Beer-Lambert is not species specific.

The mixing ratio of attenuation elements may remain relatively constant but the absolute number of those elements varies due to altitude and temperature dependent density.

The density of attenuation elements is dependent on height. The assumption of uniform density across the path is maintained … for this analysis – but the assumption of uniform density along the path is not generally valid.

The same CO2 molecule may absorb more than 1 photon; molecules may absorb photons either transmitted or reflected.

Function Sensitivity

While calculating the RX_ON/RX_OFF ratio has the advantage of nulling all common error factors – at least in theory, the result is still dependent on path-length errors.

The first part of the foundation for measurement instrumentation is the sensitivity of the measure to variations in the function parameters.

In general, the sensitivity of function y to a variation in parameter x is defined as

$\begin{displaymath}\mathbb{S}_x^y\;=\;\lim\limits_{\Delta x \to 0}\left(\,\frac{\,\dfrac{\,\Delta y\,}{y}}{\,\dfrac{\,\Delta x\,}{x}\,}\,\right)\;=\;\frac{\,x\,}{y}\,\frac{\partial y}{\,\partial x\,}\end{displaymath}$

where $\Delta$ x/x is the percent change of variable x. A sensitivity of 1 implies a 1% change in variable x will cause a 1% change in function y; a sensitivity of 0.5 implies a 1% change in x will cause a ½% change in y.

The normalized function describing the relationship between transmitted signal and received signal modified by absorption was originally derived in the form:

$\mathcal{F}\;=\;\mathit{e}^{-z\,\alpha_a}$

where z is path distance and a represents intensity attenuation.

Recalling that $\mathcal{F}$ is the measured value, the sensitivity of a function to the product of independent parameters is identical for each multiplicand – each represented below by variable x.

$\begin{displaymath}\mathbb{S}_x^{RX_{on}}\;=\;\frac{\,x\,}{\,\mathcal{F}\,}\,\frac{\,\partial \mathcal{F}\,}{\,\partial x\,}\;\;\Rightarrow\;\;-z\,\alpha\end{displaymath}$

In this case, the measurement of $\mathcal{F}$ is equally sensitive to percent uncertainties in both distance and attenuation.

Absorbance cross-sections may be considered a known physical constant [1]. To assure a measure of concentration uncertainty independent of distance requires an uncertainty of z to roughly 1/10 the desired measure uncertainty of n_a

(A measurement uncertainty in $\alpha$ of 0.25% would require a measurement uncertainty in z of roughly 0.025%: 2.5 m or less over 10 km. This is not encouraging information and is not achievable with the present implementation. Both aircraft altitude and topography uncertainties are an issue. Reflectivity is a common-mode issue and not of concern here)

Follows is a plot of total percent error against changes in percent error in height:

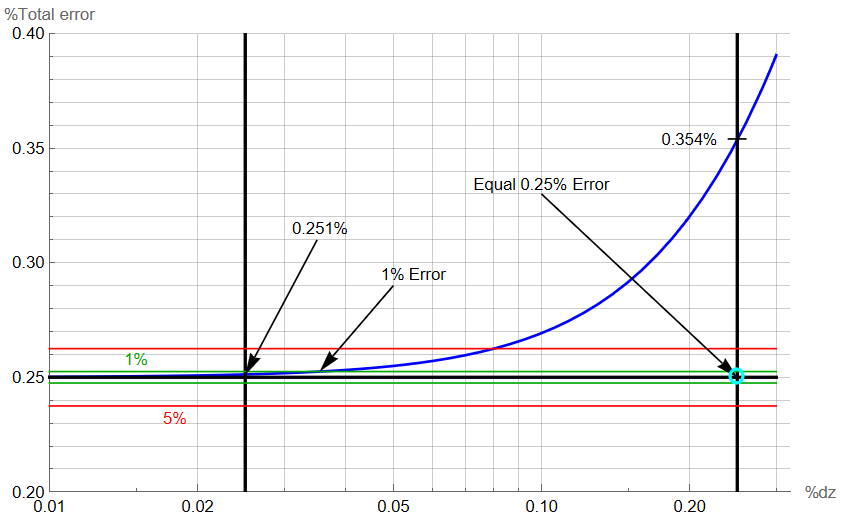
The BLU line is the total error. A small CYN circle indicates the point where both absorption and height error is 0.25%. At this point, the total error is 0.354%. If the error in z is 1/10 the error of the absorption, the total error is 0.251% (as compared to the target error of 0.25%). If a $\pm$ 1% total error is acceptable (GRN lines), the error is z needs to be less than 0.035%. The RED lines indicate a $\pm$ 5% total error.

[1] Although not truly constant, the variation of $\sigma$ is much less than the variation in the absolute values of n and z and may be considered constant for this discussion. Full analysis would require deeper knowledge of the variation than is readily available and would not contribute greatly to the results.

Optical Depth Refinement

The interest is to define instrumentation compliance and measurement range with emphasis more towards defining operational limits rather than data interpretation. The two are related in that measurement capability needs to encompass the expected variations of non-ideal variations while maintaining the capability of collecting the data to within the desired accuracy and uncertainty.

This basic derivation is based on several assumptions that fall apart for this experiment. Although the absorption cross-sections may be considered essentially constant, the absolute density of absorption particles is dependent on both temperature and altitude.

Other attenuation elements consist of various scattering particles which are not uniformly sized or distributed throughout the optical column while the volume of the optical column itself – and hence the number of potential absorption elements – has a geometry which is also dependent on distance.

Particle shadowing, multiple absorption, and asymmetric bi-directional travel paths also represent significant variations from the derivation assumptions

The previous optical depth analyses were based on uniform concentrations of both absorption and scattering particles throughout the column whereas in reality both parameters are dependent on z. Furthermore, the column is not cylindrical, a truncated cone is a better representation. While those initial assumptions may prove valid for initial estimations, the instrument will be better optimized by “fine-tuning” the approximations.

The laser beam projects throughout a volume. Within that volume, absorbing and scattering elements may interact with the photons making up the beam.

Those photons that are not scattered or absorbed are collected by a telescope and counted by the photodetector in the form of a current proportional to photon intensity

The number of photons counted is dependent on both the volume of the beam and the density of scattering and absorbing elements within that beam. Both volume and density are functions of distance – and temperature – even in the ideal Standard Atmosphere. (Note: it has been estimated that 1 of 10,000,000 photons is collected by the photodetector)

It is necessary to understand the variations and limits of these quantities before the measurement networks are considered.

It is this last item which led to the development of this discussion.

That’s all for now.

Next: Geometrical Construction

Back: Abstract

Up: Articles

Leave a Comment Cancel Reply