Looking at a page of algebraic derivations and equations is useful – almost as much so as understanding them.
But pictures are pretty …
I start with a sine wave input signal of frequency 1. The waveform is riding on a common-mode signal of 10 VDC (so that the magnitude of the waveform is entirely positive relative to GND).
One period of a sine wave. Peak value 5V riding on 10VDC. The rms value of the sine wave with no offset is 3.536 V.
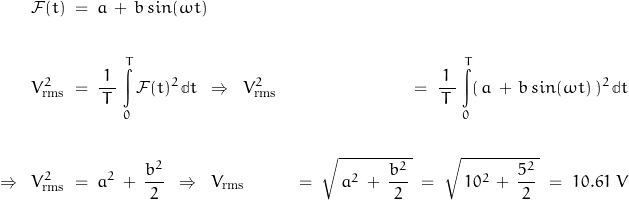
The signal-to-noise ratio is:
Here’s a representative sample of Gaussian noise.
Input parameters: Mean = 0.0 ; ![]() = 1 (RMS) ; N = 1000
= 1 (RMS) ; N = 1000
The simulation results differ though
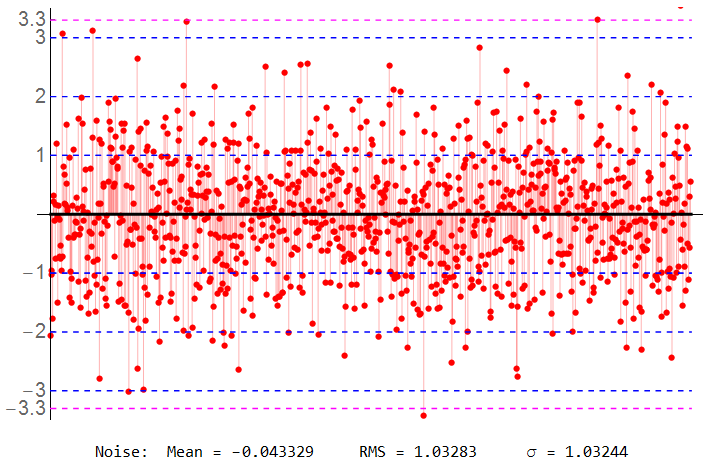
Not quite “perfect” even with 1000 samples. If I were measuring “zero volts”, I’d read an offset of 43 mV (or was the common-mode component actually 43 mV? How could I tell?)
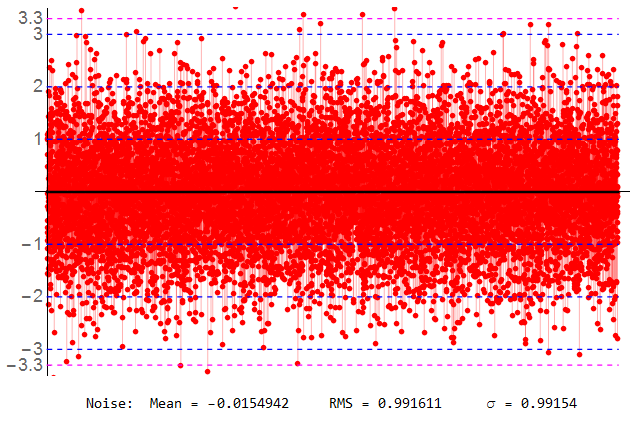
Out of curiosity, I set up a sequence of 10,007 samples (prime number).
The following are all based on the same input signal – one period of a 5 V sinewave riding on a 10 VDC offset. The rms value is 10.61 V as calculated above – the only difference in the plots is the number of samples per period.
The noise is generated with a mathematical “white noise process” of mean zero and standard deviation of 1. Each sample is independent with identical distribution. The SNR ratio for all examples is 10.61/1 or 20.5 dB.
The plots are in pairs The mean and rms value of the noise itself and the signal+noise are calculated for each data set.
Note that sample count N is effectively the over-sample factor.
N = 1000
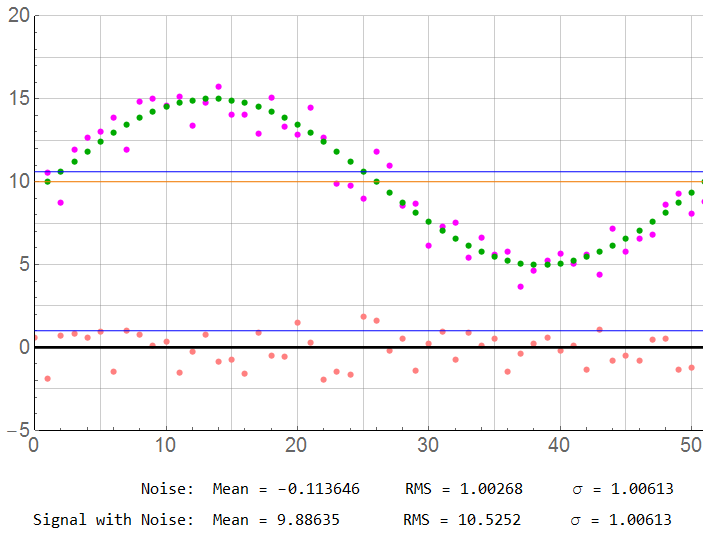
The first plot of the pair shows the ideal sampled signal along with the associated noise. The signal is indicated in GRN; the noise in RED. The BLK line at 0 is the ideal noise mean; the BLU line at 1 is the ideal standard deviation of noise. The ORG line is the DC offset of 10 V; the BLU line is the effective rms value of 10.61 V. The lower plot is the discretized noise data.
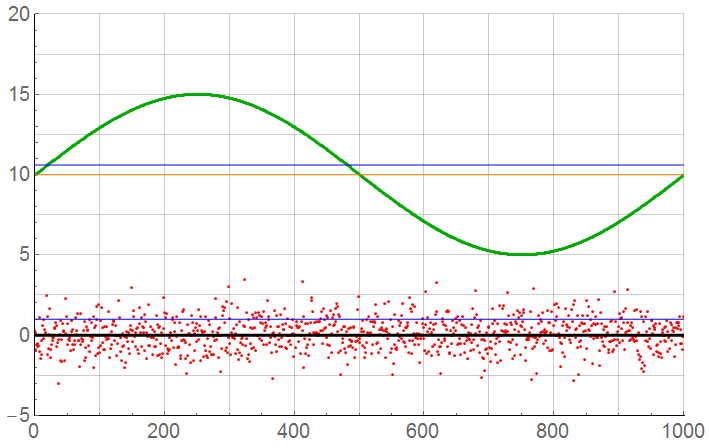
The second plot of each pair adds the noise to the signal. The MAG points are the magnitudes that would actually be digitized. The lower trace is the noise component which would not be part of the measurement. Again, the SNR is 20.5 dB. These patterns hold true for the remaining illustrations.
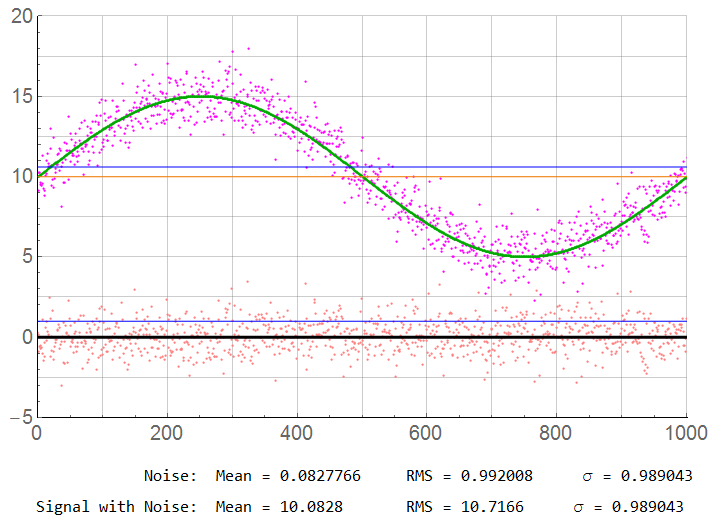
For N = 1000: Although the sample count is high, there is still possibly significant error. The “true” RMS value is 10.61; the mean should be 10.00. There is a 0.83% error … which may be acceptable in many cases. The sample rate is 500x the Nyquist limit.
N = 100
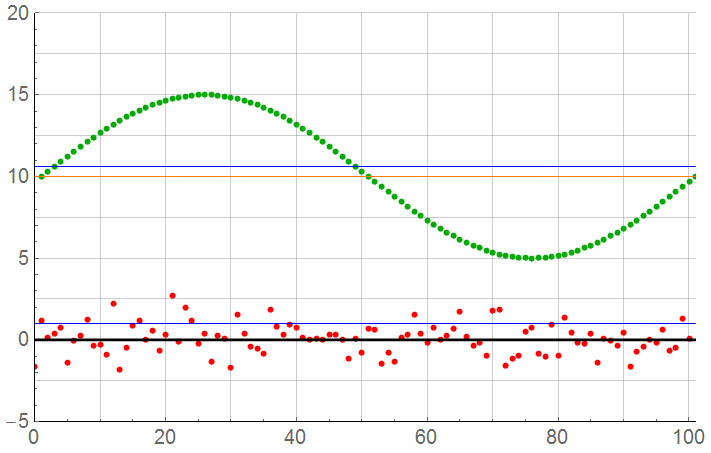
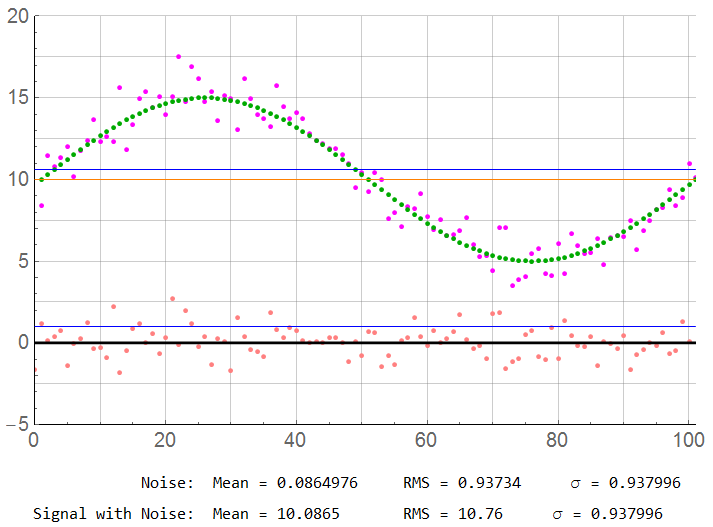
For N = 100: The sample count has been reduced by a factor of 10 but is still high. The error has increased very slightly – but an insignificant amount. The error from mean is now 0.87% … which may still be acceptable. The sample rate is 50x the Nyquist limit.
N = 50 is 25x Nyquist limit
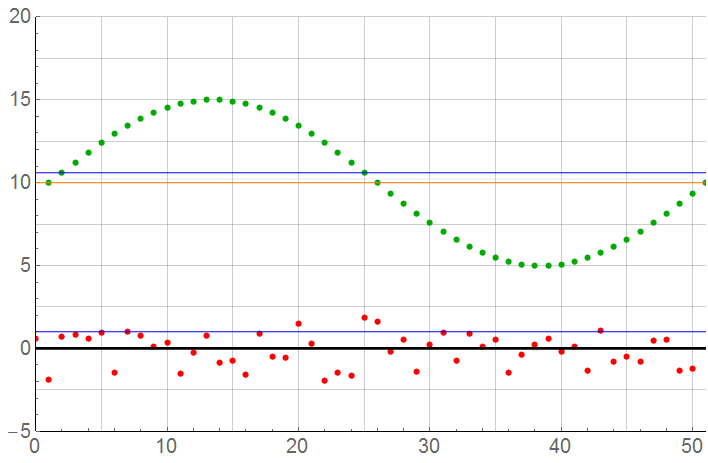
For N = 50: The sample count is now at the point where errors may not be acceptable except for crude measurements. The error from mean has now increased to 1.14% … often acceptable but better classified as “good enough” rather than accurate (which I define as 1% or better). The sample rate is 25x the Nyquist limit.
N = 20 at 10x Nyquist, many would think this sufficient
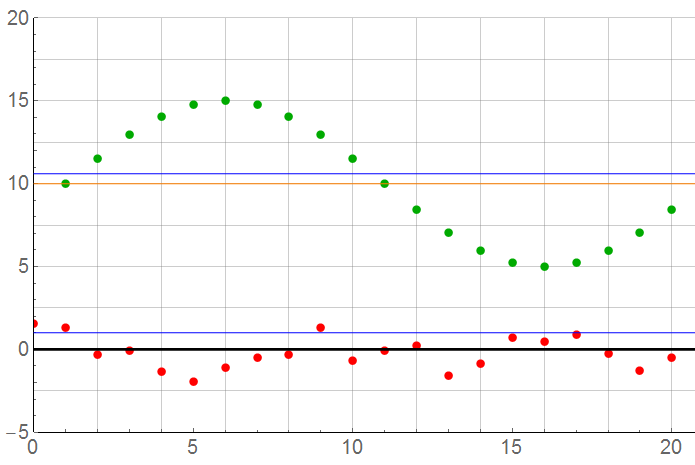
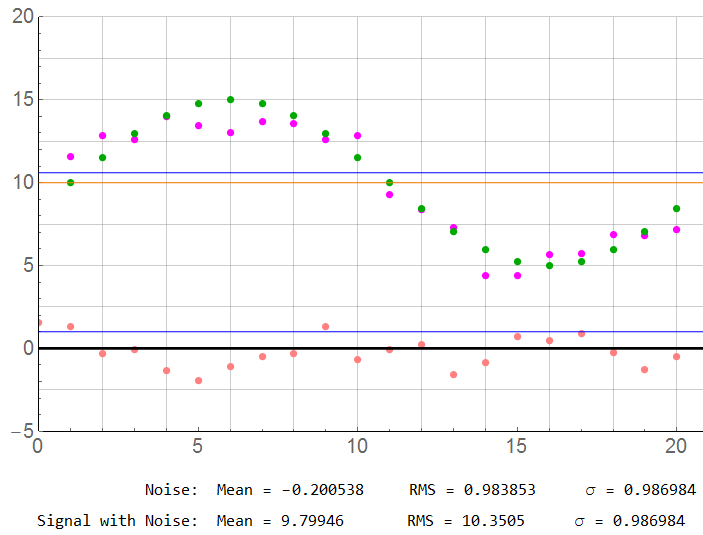
For N = 20: The sample count is now at the point where errors may not be acceptable except for crude measurements. Recall the MAG magnitudes are the measure. The error from mean now exceeds 2% … good enough? Possibly. Probably OK for a rough environment field measurement system. The sample rate is 10x the Nyquist limit.
N = 10
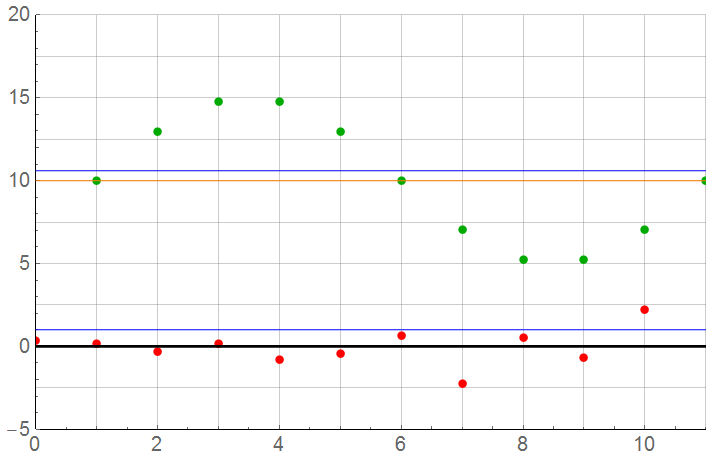
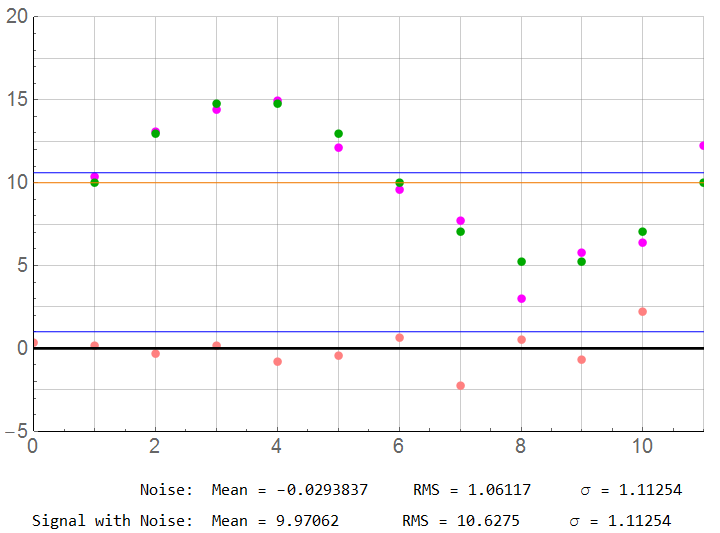
For N = 10: Borderline acceptable but the error from this particular noise set has improved to below 1%. Does this mean a sample rate of 5x Nyquist is acceptable? Recall that a higher sample rate with the same noise characteristics (and more samples averaged) resulted in errors over 2%. One sample set may be acceptably accurate; the next set may not. It would be difficult to properly interpret or develop an accurate inverse model from such data. Each data set would have an overall random error.
On the other hand, these are examples of identical information with the only variation being in independent samples of a Gaussian function – ideal for averaging. For example, I collected 24 data sets of the N = 10 signal+noise sequence. The mean value for the sum of sets was 9.91085 – less than 1% error from the mean (-0.89%). The standard deviation was 0.3367.
24 sequences of 10 samples each. 240 sample points. I also did a single sample sequence with 240 points. The mean was 10.0325 (0.33% error) with a standard deviation of 1.02423.
Consider the differences if I were collecting a single data set for each measurement environment in which that environment changed at every sample … perhaps an airplane taking geophysical measurements over a long flight path. Perhaps the terrain changes slowly (Winnipeg to Edmonton) or quickly (Las Vegas to San Francisco).
10 samples per cycle would be the lowest sample rate I’d recommend for general purposes; I’d prefer 20 to 50 samples per cycle if I want high-precision measurements. To a point, more is better.
One last example: N = 3 samples per cycle (where the Nyquist limit is 2 samples per cycle)
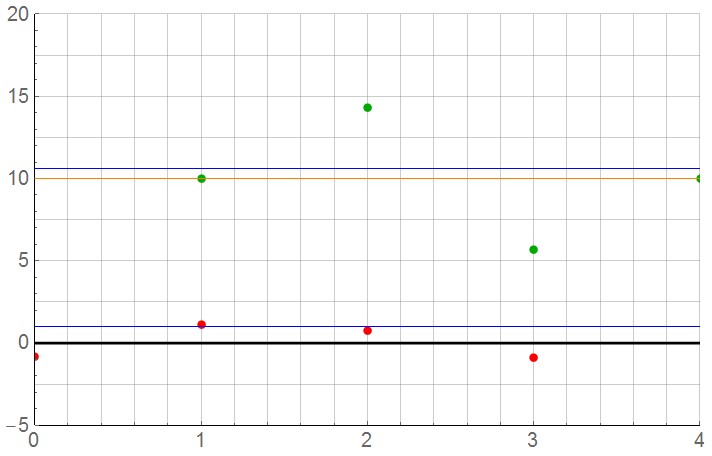
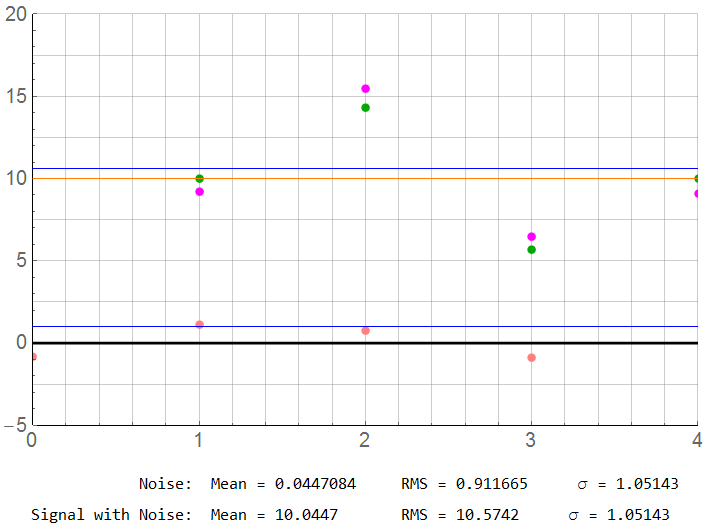
As it turn out, this is one of the more accurate results: The mean is 10.0447 (0.45% error) and standard deviation is 1.05 instead of 1.0.
When I collected a second sequence though, the mean was 9.2846 … an error of -7.2%.
A last note: I didn’t follow my own standard procedures herein, but I usually like to use prime numbers for a sample rate when I perform integer-based sampling.
That’s all for now.

Part 3
Part 5