ADC Wiggles to Bits 8.2a temp ENOB Noise free dithering averaging

Effective Number of Bits: ENOB

The effective-number-of-bits (ENOB) is the parameter that ultimately defines the resolution of measurement. All else remaining constant, additional converter bits only adds to computational effort and storage memory.

ENOB and effective resolution are not equivalent: ENOB is determined from a frequency analysis of the ADC output when the input is a full-scale sine wave of the appropriate frequency. The ENOB considers all noise and distortion with the resulting “SNR” referred to as SINAD: Signal/(Noise + Distortion)

The “effective” number of bits will often be lower than the available number of bits. The calculation of ENOB assumes an input signal at full-scale. In practice, some degree of headroom (perhaps 5 or 10%) should be allowed at the minimum and maximum portions of the range. This has the effect of reducing ENOB even further.

When noise and distortion (SINAD) as well as the signal’s maximum amplitude is considered, ENOB may be expressed:

$\begin{displaymath}\text{ENOB} \; = \; \frac{ \; \text{SINAD}_{dB} \, - \, 1.76 \, + \, 20 \, log \frac{\text{FSR}}{\; \text{SIG}_{\text{fs}} \;} \; }{6.02}\end{displaymath}$

where $\text{SIG}_{\text{fs}}$ is the signal full-scale amplitude.

As an example:
Assume a 12-bit converter with FSR = 1. The RMS value of a sine wave having PP amplitude of 1V is:

$\begin{displaymath}V_{rms} \; = \; \frac{V_{pp}}{\, 2 \, \sqrt{\, 2 \, } \, } \; = \; \frac{1}{\, 2 \, \sqrt{\, 2 \, } \, } \; = \; 0.3535 \, V\end{displaymath}$

The allowable RMS uncertainty V $_{u,RMS}$ expressed as a function of of required bits can be determined from:

$\begin{displaymath}V_{u,rms} \; = \; \frac{V_{in,rms}}{\, 6.02 \, N_{eff} \, + \, 1.76 \, }\end{displaymath}$

For a sine input voltage exactly matching the ADC FSR of above, the maximum allowable RMS uncertainty is:

$\begin{displaymath}log \, V_{u,rms} \; = \; log \, V_{in,rms} \, - \, \frac{\, 6.02 \, N_{\text{eff}} \, + \, 1.76 \, }{20}\end{displaymath}$

For 12-bits of effective resolution, the RMS uncertainty needs to be constrained to 70.5 $\mu$ V

So what are the components of that uncertainty?

The quantization noise is straight-forward – this is a function of converter resolution; ie:

$\begin{displaymath}V_{n,Q} \; = \; \frac{ \, V_{\text{LSB}} \, }{\, \sqrt{\,12 \, }\,}\end{displaymath}$

where V $_{\text{LSB}}$ is defined as:

$\begin{displaymath}\text{LSB} \; = \; \frac{ \, \text{FSR} \, }{2^N}\end{displaymath}$

For the example 12-bit ADC with FSR = 1V:

$\begin{displaymath}\text{LSB} \; = \; \frac{ \, 1 \, }{2^\text{12}} \; = \; \oldstylenums{244.1} \; \mu \text{V}\end{displaymath}$

$\begin{displaymath}V_{n,Q} \; = \; \frac{ \, \oldstylenums{244.1} \; \mu \text{V} \, }{\, \oldstylenums{3.464} \,} \; = \; \oldstylenums{70.5} \; \mu \text{V}\end{displaymath}$

Hm-m-m … the error budget is used up just from quantization error; there’s no room for additional uncertainty.

Consider a system with ideal FSR of 1V and RMS uncertainty of 1 mV (admittedly a large amount of uncertainty)

$\begin{displaymath}\text{SNR} \; = \; \dfrac{ \, \frac{\, V_p \,}{\, \sqrt{2} \, } \, }{\,\frac{\, V_{LSB} \, }{\, \sqrt{12} \, } \, } \; \; \Rightarrow \; \; \dfrac{ \, \frac{\, 0.5 \,}{\, \sqrt{2} \, } \, }{\,0.001 \, } \; = \; 353.6 \; \; \Rightarrow \; \; 51.0 \; dB\end{displaymath}$

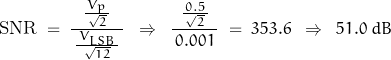
The effective number of bits (ENOB) is:

$\begin{displaymath}N \; = \; \frac{ \, 51.0 \, - \, 1.76 \, }{6.02} \; = \; 8.17 \; \rightarrow \; 8 \; bits\end{displaymath}$

… regardless of the inherent ADC resolution.

For 12-bit resolution at 1V FSR, the noise needs to be less than 70.5 μV; less than 4.4 μV for 16-bit.

Note that this calculation assumes ideal full-scale signals with no more than ±½ LSB error, no additional noise sources, and no spectral distortion.

Common usage sometimes implies that SNR is equivalent to dynamic range. While they overlap, the value of SNR defines the maximum range of resolvable information – assuming noise “N” represents the minimum resolvable signal and DR defines the dynamic range of the signal – the range between the minimum and maximum signal. They are both calculated in the same manner but while DR may be equivalent to SNR, it shouldn’t be larger – and should be smaller.

Noise-Free Count

To further refine and confuse the issue, the concept of “noise-free count” is introduced.

The noise-free code resolution is the number of bits beyond which it is impossible to distinctly resolve individual codes. Noise is is expressed as an RMS quantity but bits are toggled by peak-to-peak variation. Gaussian RMS noise is converted to PP noise by multiplying the RMS value by 6 or so¹.

While a 12-bit converter may have 4096 counts, a good many of them may represent noise and be of little use. The noise-free count is the number of counts available after removing those representing various uncertainties.

The noise count is determined from the number of bits encompassing the PP noise:

$\begin{displaymath}\text{count} \; = \; \frac{2^N}{\, N_{LSBpp} \, }\end{displaymath}$

Effective resolution is often defined using $\text{SNR} \, = \, \text{FSR/N}_{rms}$ but this value over estimates the resolution by a factor of $log_2(6.6) \; \Rightarrow \; 0.3673$

$\begin{displaymath}\text{count}_{\text{eff}} \; = \; \frac{\, FSR \,}{\, N_{rms} \, } \, - \, log_2 (6.6)\end{displaymath}$

Averaging is often used to decrease the effects of noise. Averaging 2 samples will improve SNR by 3 dB but reduces the effective sample rate by half. It takes the average of 4 samples to increase resolution by 1 bit but decreases the effective sample rate by 1/4. It takes 16 samples to increase the resolution by 2 bits – which slows the effective sample rate by a factor of 4.

1 LSB remains the limit of resolution, averaging does not improve linearity, and the low frequency effects of 1/f noise may actually increase noise by the same factor that averaging is intended to improve it (V $_{\text{n}} \times \sqrt{\, N \,}$ ). Averaging also requires additional memory and computational resources.

Dithering

“Dithering” is a process which increases the accuracy of the resulting word through the process of averaging. If a controlled amount of additional noise is added to the input – a value a bit over ½LSB … perhaps 2/3 LSB? – the signal has a pp amplitude of 3 LSB. The digital word toggles between values. This might be accomplished by adding a controlled source of random numbers to a DAC and injecting the result into the input signal. After quantization, the post-processing can subtract the injected portion of the signal from the digital output, ideally resulting in the desired digital representation of the input. This can aid in the resolution of a “constant” input (near-DC with reference to the sample frequency) but may not reduce the effects of additional uncertainties

Consider a constant input voltage of 0.5001 V to a 1000 count converter ( counts 000 → 999) with FSR = 1V. This input value lies 1/10 of the magnitude between count 500 and 501. If 1000 samples were collected, the result would be 1000 identical digital words of 500. If dithering were appropriately applied, roughly 900 words would be 500, the remaining 100 words having value of 501. When averaged, the result would be near 500.1 as desired.

But consider: the desired resolution is 100 ppm. A 1000 count converter does not have this resolution. The proposed solution is developed based on a noiseless constant signal, exactly matched to the ideal transition point. In order to perform the desired function, additional circuitry and software need to be added to the system, additional post-processing is required, and the effective sample period has been extended by a factor of 1000.

While this may be suitable for some applications, it may be an inappropriate solution for signals not fitting the expressed assumptions.

Averaging – ADC

The number of effective bits – resolution – in an ADC may be often increased by averaging. In the ideal case, the improvement is a function of the square root of K where K may be the number of sequential samples or the number of parallel simultaneous paths.

Parallel sampling is not generally practical at the discrete circuit level. The implementation requires each parallel signal path be identical: a full network – amplifiers, filters, ADCs, etc – matched for each path. Potentially useful at the integrated level, an analysis of this method is not discussed herein.

One limitation is the necessity for converter linearity to be within an acceptable limit of the improved resolution. Ideally, two adjacent codes are averaged to result in a new code falling halfway between the two original codes. If the converter is non-linear, the new code may not represent significant improvement. If the converter has a missing code , averaging has no effect; if the converter is not monotonic, the average value is inaccurate.

Consider a sequence of samples in BLU:

Under ideal conditions, the continuous signal (in CYN) is quantized at exact discrete code levels. By averaging the sequential discrete sample codes (in BLU) the effective resolution is increased through the creation of discrete pseudo-levels (RED).

The apparent effectiveness of this method suggests that a low-resolution ADC be implemented with the required increase in resolution accomplished with digital averaging. While feasible to a degree, several necessary requirements for this process need to be met for this method to work.

The sample rate is not increased in the sequential sample averaging as it could be in the parallel scheme.

While changing the sample frequency doesn’t change the RMS value of quantization noise

(this is 2 parallel paths)

The effects of noise can be reduced by averaging. Consider a 16-bit converter with 14 noise free bits sampled at 1MHz (1 MS/s). Averaging two samples increases the SNR by 3 dB but reduces the effective data rate to 500 kHz (500 kS/s). Averaging four samples increases the SNR by 6 dB, reduces the data throughput to 250 kS/s, and increases the resolution by 1 bit. It takes 16 samples to increase the resolution by 2 bits – at an effective data rate of 62.5 kS/s.

This technique can be effective if the reduction in data rate in conjunction with the additional computational effort and memory can be tolerated. Note that this technique does not improve linearity. Averaging will not improve the resolution below 1 LSB.

Effective number of bits (ENOB) and effective resolution are not equivalent: ENOB is properly determined from an FFT analysis of the ADC output when the input is a full-scale sine wave. The ENOB considers all noise and distortion with the resulting “SNR” referred to as SINAD: Signal/(Noise + Distortion)

There are two significant limitations to an “accurate” conversion: the noise and distortion introduced by the networks before the ADC input and the internal ADC networks. “Dithering” is a technique which may prove useful in reducing inherent non-linearity of the ADC. This is accomplished by adding about ½ LSB “white” noise to the input signal. This noise tends to randomize the input minimizing correlation between quantization noise and input when the input is at some sub-multiple of the sample frequency. Most systems contain enough noise already; adding additional noise will reduce SNR. The effectiveness is highly dependent on the application, associated networks, and the ADC used.

55555555555555555555555555555555555

Reviewing the expression for RMS:

$\begin{displaymath}V_{\text{RMS}} \; = \; \sqrt{ \, \int\limits_{fL}^{fH} V^2(f) \, df \, } \; = \; V_n(0) \, \sqrt{ \, fh \, - \, fL \, }\end{displaymath}$

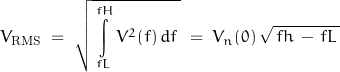
It is obvious that integration is involved. The same may be said for averaging:

$\begin{displaymath}F_{\text{avg}} \; = \; \frac{1}{\, N \, } \, \sum\limits_{i=1}^N X_i \quad \Leftrightarrow \quad F_{\text{avg}} \; = \; \frac{1}{\, b \, - \, a \, } \, \int\limits_{fL}^{fH} F(x) \, dx\end{displaymath}$

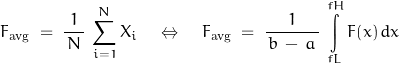
Although averaging is a common method to decrease uncertainty, consider that the conversion process is in effect a short period integration. The effect on bandlimited voltage noise with a normal distribution can be expressed by integrating the variance of noise.

$\begin{displaymath}V_{\text{n,RMS}}^2 \; = \; \int\limits_{fL}^{fH} V^2(f) \, df \; = \; V_n(0) \, \left( \, \frac{1}{\, fH \,} - \, \frac{1}{\, fL \, } \, \right)\end{displaymath}$

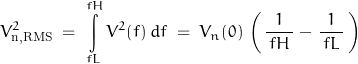
3333333333333333333333333333333

Averaging Spectral Density

The effects of averaging can be visualized by examining the changes in RMSenergy density as effective time increases. The energy density is constant; as time increases, magnitude deceases. Normalizing to a single sample (BLU), averaging two samples – effectively doubling the sample time – will reduce the magnitude by 1/ $\sqrt{2}$ . Doubling that – sample time is now four units – reduces the magnitude to ½.

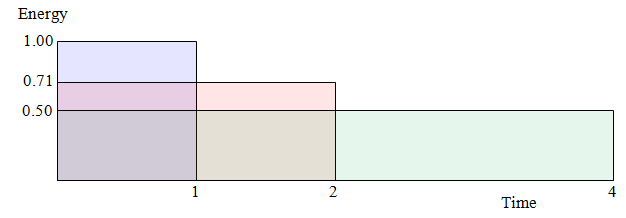
3333333333333333333333333333333

I don’t wish to get deep into the details of the typical ADC but I thought it might be nice to briefly mention some of the more common non-ideal aspects of a practical ADC.

Zero Offset Error
Zero-scale offset is the difference of the actual first transition level and the ideal level. Basically, is zero actually zero? It’s a constant value and may be calibrated out – if the manufacturer hasn’t built the correction into the device (likely by laser trimming)

Full Scale Offset Error
Essentially the same concept as zero offset error: Is the full-scale transition point where it should be?

Gain Error
The deviation of the transfer slope from the ideal.

Integral Non-Linearity (INL)
A large scale error describin the “straightness” of the transfer curve. This may be measured by a “best-fit” which may offset the transfer at the extremes, or by fitting a straight line to the end points. The transfer curve near the end points is closer to the ideal, but the middle range may suffer. However, the end-point fit gives worst-case error and is more appropriate to compare errors of different ADCs.

Differential Non-Linearity
This error causes missing codes as the difference between transition points may vary. If the error is 1 LSB or more, output codes may be missed. This is a small scale error relating to variations in step size.

Total Harmonic Distortion (THD)
Describes the linearity on the basis of harmonic components. A pure sine wave should have no harmonics; a pure square wave should only have odd harmonics with specific amplitudes at each harmonic.

Spurious Free Dynamic Range (SFDR)
The difference in RMS amplitude between the desired signal and any output frequency not present at the input.

Intermodulation Distortion (IM)
Non-linearity in the transfer function will cause intermodulation of a signal with two or more frequencies components.

Other items to consider:
Power supply decoupling
Reference voltage decoupling
External noise sources
Clock noise
Leakage between output and input

That’s good for now.

¹For a Guassian distribution of mean 0 and standard deviation 1, the RMS value is also 1. However, the ADC converts based on peak-to-peak values, the limits of which are defined by ± some value of $\sigma$ . 84.1% of all samples will have values between ±1 $\sigma$ , 97.7% between ±2 $\sigma$ , 99.87% between ±3 $\sigma$ , 99.95% between ±3.3 $\sigma$ , and 99.997% between ±4 $\sigma$ . The specific number selected is basically personal choice – the distribution won’t be purely Gaussian anyway and the actual noise level will be a bit higher than a Gaussian analysis predicts.

Noise-Free Count

Dithering

Averaging – ADC

More

Averaging Spectral Density