ADC
Ultimately, the information will need to be quantized. In an ideal situation, a 10-bit ADC has resolution of 1 part per 1024 – approximately 0.1% – which would be sufficient to quantize information to 0.25%. 12-bit ADCs resolve 1 part of 4096 (0.024%) and are readily available in rad-hard components. A 16-bit ADC does not gain much: the majority of information is noise … and as will be discussed, “averaging” is not always an effective means of reducing noise not of a Gaussian distribution.
The problem comes about from defining an efficient use of bits …
I remind myself that I’m still working with an “ideal” linear system. The signals are of mathematical sine waves and there is no noise or distortion.
I want to pass over the interface networks for the moment and proceed directly to the ADC. The requirements of the ADC performance help define the requirements of the interface networks. While there are minor variations in ADC operation, the mapping of analog-to-binary follows a pattern similar to this illustration of a 4-bit device.
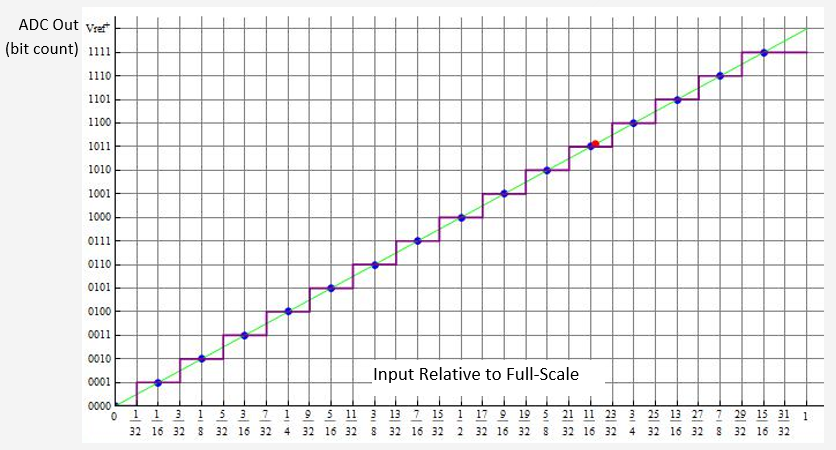
The vertical PUR line represents the transition points; voltages along the horizontal sections of the PUR line are deemed identical by the quantization process. The GRN line represents the “ideal” linear response; the BLU dots represent the “ideal” conversion points; the RED dot an illustrative arbitrary input level – in this illustration of a 4-bit system, an input voltage of 0.6938V is mapped to a binary representation of 1011. Transitions occur at the ½-LSB level between steps.
An ADC (usually) linearly scales an input voltage signal between some minimum and maximum level. This can be mapped as bits vs voltage as shown below for a 16-bit converter. This particular diagram scales the normalized range of intensity to bit count (where “0.4” represents no abnormal CO2 absorption)
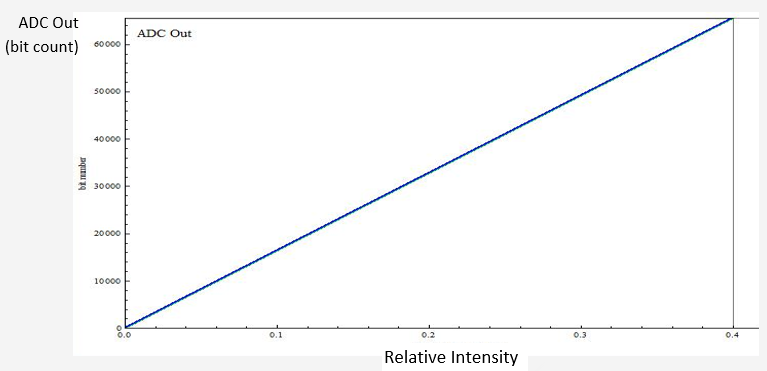
Although the BLU line in this illustration consists of (65,536) discrete steps, they don’t show as such at this scale. The vertical scale is bit number: 0 ® 65535
The stated goal is to measure 1ppm/m3 of CO2. Since a nominal value of CO2 is approximately 380ppm in the atmosphere, this BOE analysis will assume a measurement resolution of 1 part in 380 meets the criteria. This is equivalent to about 0.26%.
For illustrative purposes, consider the following:
The relative amplitude resulting from a 0.3% change in CO2 over a distance of 10km (the entire column) is 0.3989. This is a difference in amplitude of 1.0978E-3 and the ADC output is 1111 1111 0100 1100.
On the other hand, a plume having a 1% increase of CO2 100m thick at 1km above ground will have a relative amplitude of 0.399963 with a difference from nominal of 36.65E-6 and an ADC output of 1111 1111 1111 1001
However, this experiment is configured to only measure the result of integration of the entire column (as it is assumed the common-mode signal contains various reflectivity and scattering components which are nullified in the processing)
The majority of signal applied to the ADC does not contain useful information as the common-mode portion of the signal is also processed. Very small variations in CO2 will only affect the upper-most bits; a 50% variation on CO2 over the entire measurement path maps to the ADC as:
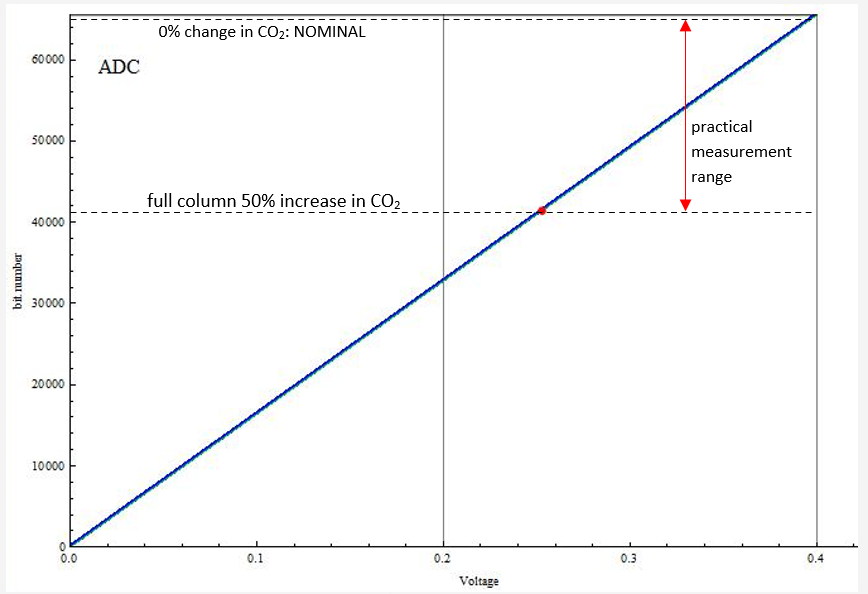
where the RED dot represents the normalized ADC input (with ADC output of 1010 0001 1110 1100)
– this corresponds to bit 41452 of 65536
This approach
I look at this in more depth later on. However, this exercise provides an idea of the parameters necessary to make these measurements. Using these assumptions, this measurement can be made although much capability is wasted. The next step is to consider the differences between mathematical representations and physical implementation.
*****************************************
Exponential Signals
The basic information to be measured was demonstrated earlier to be of the form
Assume ideal mapping of this signal to the ADC.
The direct linear mapping of the signal to the ADC has an error proportional to time and inversely proportional to amplitude due to the asymptotic nature of the exponential signal: ie, as time increases and amplitude decreases, the signal is compressed into the lower bits of resolution. Signal information is lost in quantization error.
This is illustrated with the figures below (using 3-bit quantization for clarity)
Here it can be seen that all information occurring at times greater than about t = 5 is lost in quantization
( when normalized, 1LSB16 ~ 15E-6 ; 1LSB12 ~ 244E-6 )
If I linearize this signal, I get the following ADC mapping
Each quantization level contains an equal degree of signal information.
Furthermore, the 0 LSB is decreased to a point of t > 8 so that more low-level information is available Consider that the intensity dynamic range may be on the order of 4-5 decades, it should be obvious that a linear mapping will require truncation of the high levels of signal to expand the low-level signals … or a loss of low-level information to prevent saturation due to high-level signals. In order to adequately measure “1ppm”, differential signal variations are expected to be on the low-side of the range.
Next: TBD
Back 9: Photodiodes & Signal Range
Up: Articles
