Distributed Parameters 8 – Lumped Parameter

Consider a short-circuited distributed RC section represented by N identical sections. A unit-step is applied at the input and we’d like to determine the current in the nth section

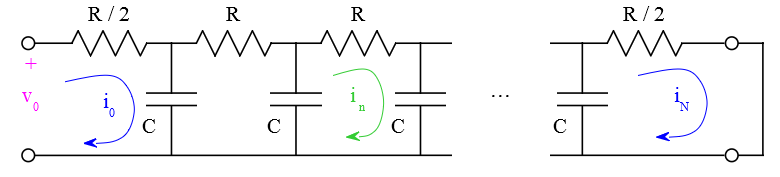
It was previously shown that the current for an RC line is:

$\begin{displaymath}I_n(s)\;=\;V_o(s)\,\frac{\mathit{cosh}(N-n)\,\tau}{\,Z_b\,\mathit{sinh}\tau\,\mathit{sinh}N\,\tau\,}\end{displaymath}$

where $Z_b\,=\,\frac{1}{\,C\,s\,}$ and $\tau\,=\,\mathit{cosh}^{-1}\left(\,1\,+\,\frac{Z_a}{\,Z_b\,}\,\right) \,=\,\mathit{cosh}^{-1}\left(\,1\,+\,\frac{\,R\,C\,s\,}{2}\,\right)$

With a unit step input:

$\begin{displaymath}I_n(s)\;=\;\frac{1}{\,s\,}\,\frac{\,C\,s\,\mathit{cosh}(N-n)\,\tau\,}{\mathit{sinh}\tau\,\mathit{sinh}N\,\tau\,}\end{displaymath}$

The poles of this equation are at $\mathit{sinh}\tau\,\mathit{sinh}N\,\tau\;=\;0$

Using the identity for the hyperbolic sin, the roots can be found from:

$\begin{displaymath}2^{N-1}\,\mathit{sinh}^2\tau\,\prod_{n=1}^{N-1}\left(\,\mathit{cosh}\tau\,-\,\mathit{cos}\frac{\,n\,\pi\,}{N}\,\right)\;=\;0\end{displaymath}$

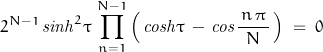
Indicating N+1 simple roots (on the $\sigma$ axis)

Some wiggling of expressions gives:

$\begin{displaymath}i_n(t)\;=\;\frac{1}{\,N\,R\,}\,+\,\frac{2}{\,N\,R\,}\,\sum_{k=1}^{N-1}\,\left[\,\mathit{cos}\left(\frac{\,k\,\pi\,}{N}\,\right)\,\mathit{e}^{s_k t}\,+\,\frac{\:(-1)^n\,}{N\,R}\,\mathit{e}^{4 t/R C}\,\right]\end{displaymath}$

The transient response of the distributed network may be found by considering the following network. m.ake the assumption that G/C is a constant.

The network equation is given as:

$\begin{displaymath}V_{out}\;=\;V_{in}\,\frac{Z_{21}\,R_L}{\,\left(\,Z_{11}\,+\,R_S\,\right)\,\left(\,Z_{22}\,+\,R_L\,\right)\,-\,Z_{12}^2\,}\end{displaymath}$

where the transient response to a unit-step input would be found from:

$\begin{displaymath}V_{out}\;=\;\frac{1}{\,s\,}\,\frac{Z_{21}\,R_L}{\,\left(\,Z_{11}\,+\,R_S\,\right)\,\left(\,Z_{22}\,+\,R_L\,\right)\,-\,Z_{12}^2\,}\end{displaymath}$

Thin-Film Resistor

One of the common uses of distributed parameter analysis is in passive elements of integrated circuits. The dimensions of the circuit are such that resistive conductors often have significant capacitance distributed along the conductor.

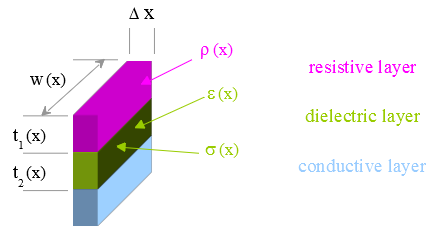
An illustrative cross-section is shown:

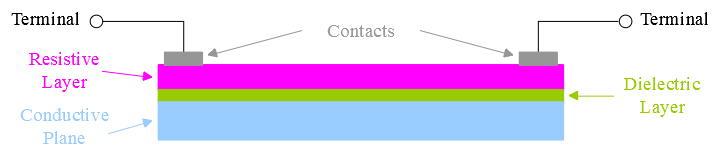
Assume a geometry such that the network consists of a one-dimensional current flow. The conductive resistance contains the current; the dielectric layer is representative of perhaps a layer of SiO₂ or a depletion region separating the resistive layer from another conductive or semiconductive layer.

The equivalent network is often symbolized as:

and the incremental network can be represented as:

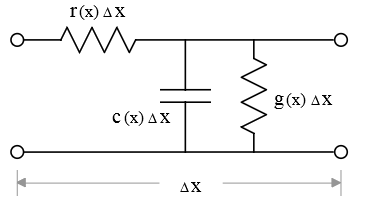
The network equations can be related to an incremental segment of the physical structure:

The incremental resistance of the structure is given as:

$\begin{displaymath}r(x)\,\Delta x\;=\;\dfrac{\,\rho\,\Delta x\,}{w\,t_1}\end{displaymath}$

where ρ is the resistivity of the material and t₁ is the thickness of the layer at x. w is the width of the resistive element at x.

The dielectric is assumed lossy – g(x) ≠ 0 – with an incremental capacitance where

$\begin{displaymath}\begin{align}c(x)\,\Delta x\;&=\;\frac{\,w\,\varepsilon\,\Delta x\,}{t_2}\quad\textnormal{where}\;\;\varepsilon\;\textnormal{is the dielectric permittivity}\\\\g(x)\,\Delta x\;&=\;\frac{\,w\,\sigma\,\Delta x\,}{t_2}\quad\textnormal{where}\;\;\sigma\;\textnormal{is the dielectric conductivity}\end{align}\end{displaymath}$

and t₂ is the thickness of the dielectric layer.

As $\Delta x\,\rightarrow\,0$

$\begin{displaymath}\begin{align}r(x)\;&=\;\frac{\,\rho\,}{\,w\,t_1\,}\\\\c(x)\;&=\;\frac{\,w\,\varepsilon\,}{t_2}\\\\g(x)\;&=\;\frac{\,w\,\sigma\,}{t_2}\end{align}\end{displaymath}$

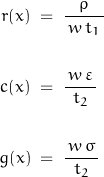
r(x), c(x), g(x) are all real, positive, and finite. These characteristics help define the differential solutions. In many cases, g(x) is considered to be zero.

The current-voltage relationship may be expressed as:

$\begin{displaymath}\begin{align}\frac{\,d V(s,x)\,}{d x}\;&=\;-r(x)\,I(s,x)\\\\\frac{\,d I(s,x)\,}{d x}\;&=\;-[\,s\,c(x)\,+\,g(x)\,]\,V(s,x)\;\;\Rightarrow\;\;\frac{\,d I(s,x)\,}{d x}\;=\;-s\,c(x)\,V(s,x)\,\big|_{g(x)\rightarrow 0}\end{align}\end{displaymath}$

Following through with the differentiation

$\begin{displaymath}\begin{align}V"\,-\,\frac{\,r'\,V'\,}{r}\,-\,s\,r\,c\,V\;=\;0\;\;&\Rightarrow\;\;\frac{d}{\,d x\,}\,\left[\,\frac{1}{\,r(x)\,}\,\frac{\,d V\,}{d x}\,\right]\,-\,s\,c(x)\,V\;=\;0\\\\I"\,-\,\frac{\,c'\,I'\,}{c}\,-\,s\,r\,c\,I\;=\;0\;\;&\Rightarrow\;\;\frac{d}{\,d x\,}\,\left[\,\frac{1}{\,s\,c(x)\,}\,\frac{\,d V\,}{d x}\,\right]\,-\,r(x)\,I\;=\;0\end{align}\end{displaymath}$

That’s good for now. Next: Boundary Effects

Leave a Comment Cancel Reply