Distributed Parameters 6 – T-Network Taylor Series Expansion

Consider a function of the form:

$\begin{displaymath}V"\,-\,\frac{\,Z'\;}{Z}\,V'\,-\,Y\,Z\,V\;=\;0\end{displaymath}$

There exists a Taylor Series Expansion such that for any point p for p between 0 and d, the voltage can be expressed as:

$\begin{displaymath}V(p\pm h)\;=\;V(p)\,\pm h\,V'(p)\,+\,\frac{\;h^2\,V"(p)\;}{2!}\,+\,\cdots\end{displaymath}$

The approximation is made by taking the values of V(x) at x = p and x = p $\pm\,\Delta$ p where $\Delta$ p is some incremental length of the network:

$\begin{displaymath}\begin{align}V'(p)\;&\approx\;\frac{\;V(p+\Delta p)\,+\,V(p-\Delta p)\;}{2\,\Delta p}\\\\V"(p)\;&\approx\;\frac{\;V(p+\Delta p)\,+\,V(p-\Delta p)\,-\,2\,V(p)\;}{(\,2\,\Delta p\,)^2}\end{displaymath}$

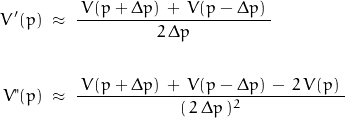
The approximate solution of the network equation may now be expressed:

$\begin{displaymath}\left(\,2\,-\,\dfrac{\,Z'\;}{Z}\,\Delta p\,\right)\,V(p+\Delta p)\,+\,\left(\,2\,+\,\dfrac{\,Z'\;}{Z}\,\Delta p\,\right)\,V(p-\Delta p)\,-\,\left[\,4\,+\,2\,(\Delta p)^2\,Y\,Z\,\right]\,V(p)\;=\;0\end{displaymath}$

with the solution represented by:

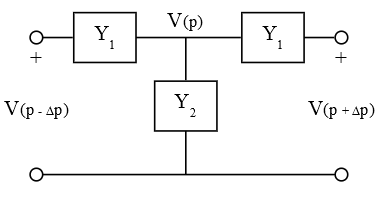
where:

$\begin{displaymath}\begin{align}Y_1\;&=\;\frac{1}{\,\Delta p\,Z(p)\,}\,+\,\frac{\,Z'\;}{\,2\,Z^2(p)\,}\;\approx\;\frac{1}{\;\Delta p\,\left[\,Z(p)\,-\,\dfrac{\,\Delta p\,}{2}\,\right]\,}\;\approx\;\frac{1}{\,\Delta p\,Z_1\,}\\\\Y_1\;&=\;\Delta p\,Z(p)\\\\Y_3\;&=\;\frac{1}{\,\Delta p\,Z(p)\,}\,-\,\frac{\,Z'\;}{\,2\,Z^2(p)\,}\;\approx\;\frac{1}{\;\Delta p\,\left[\,Z(p)\,+\,\dfrac{\,\Delta p\,}{2}\,\right]\,}\;\approx\;\frac{1}{\,\Delta p\,Z_3\,}\end{align}\end{displaymath}$

This T-network has admittance Y₁ between points x = p – Δp and x = p. The admittance Y2 is the average per unit length shunt admittance between points [ p – (Δp)/2 ] and [ p + (Δp)/2 ] multiplied by Δp.

That’s good for now. Next: Transient and Frequency Respons e

Leave a Comment Cancel Reply