Consider a distributed RC network where:
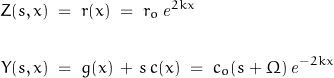
Define: ![]()
and let ![]()
That was the simple part …
The first set of coefficients:
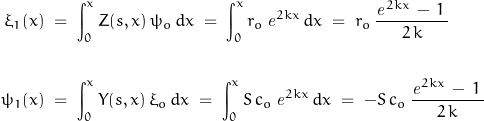
On to the 2nd:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}\xi_2(x)\;&=\;\int_0^x Z(s,x)\,\psi_1\,d x\;=\;\int_0^x r_o\,\mathit{e}^{2kx}\,\left[\,S\,c_o\,\frac{\,V\,-\,1\,}{2\,k}\,\right]\,\,d x\\\;&=\;\frac{S\,\tau}{\,(2\,k)^2\,}\,\left(\,\mathit{e}^{2kx}\,-\,2\,k\,x\,-\,1\,\right)\\\\\psi_2(x)\;&=\;\int_0^x Y(s,x)\,\psi_1\,d x\;=\;\int_0^x c_o\,\mathit{e}^{2kx}\,\left[\,r_o\,\frac{\,V\,-\,1\,}{2\,k}\,\right]\,\,d x\\\;&=\;\frac{S\,\tau}{\,(2\,k)^2\,}\,\left(\,\mathit{e}^{2kx}\,-\,2\,k\,x\,-\,1\,\right)\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-65eea62f4527aa6c335c5e0f3c98e299_l3.png)
And on to the 3rd:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}\xi_3(x)\;&=\;\frac{\;S\;\tau\;r_o\;}{\,(2\,k)^2\,}\,\int_0^x \,\left(\,\,1\,+\,\,2\,k\,x\,\mathit{e}^{2kx}\,-\,\mathit{e}^{2kx}\,\right)\,dx\,\;=\;\frac{\;S\;\tau\;r_o\;}{\,(2\,k)^3\,}\,\left[\,\,2\,+\,\,2\,k\,x\,-\,\mathit{e}^{2kx}\,(\,2-\,2\,k\,x\,)\,\right)\,\right]\\\\\psi_3(x)\;&=\;\frac{\;S\;\tau\;c_o\;}{\,(2\,k)^2\,}\,\int_0^x \,\left(\,\,2\,k\,x\,\mathit{e}^{2kx}\,-\,\mathit{e}^{2kx}\,-\,1\,\,\right)\,dx\,\;=\;\frac{\;S\;\tau\;r_o\;}{\,(2\,k)^3\,}\,\left[\,-\,2\,+\,\,2\,k\,x\,+\,\mathit{e}^{2kx}\,\left(\,2\,+\,2\,k\,x\,)\,\right)\,\right]\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-1c9072095f09336c5988dbe47a580bf0_l3.png)
And on to the … oh, never mind. Believe me, it goes on …
Voltages ![]() and
and ![]() are now found:
are now found:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}V_A(s,d)\;&=\;\sum\,\xi_{2n}(d)\;=\;1\,+\,\xi_2(d)\,+\,\xi_4(d)\,+\, ...\\\\&=\;1\,+\,\frac{\;S\;\tau\;}{\,(2\,k)^2\,}\,\left(\,\mathit{e}^{2kx}\,-\,2\,k\,d\,-\,1\,\right)\,+\,\frac{\;S^2\;\tau^2\;}{\,(2\,k)^4\,}\,\left[\,(2\,k\,d)\,\mathit{e}^{2kx}\,+\,3\,2\,(2\,k\,d)\,+\,\frac{\,(2\,k\,d\,)^3\,}{2!}\,\right]\,+\,\cdots\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-186dcf22865d5e9629156f72d7b19e62_l3.png)
Some righteous algebraic nightmares there, eh?
So, continuing on …
The results of a similar procedure for a lossless LC network are:
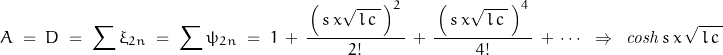
![Rendered by QuickLaTeX.com \begin{displaymath}B\;=\;\sum \xi_{2n-1}\;=\;\sqrt{\,\frac{l}{\,c\,}\,}\,\left[\,s\,x\,\sqrt{\,l\,c\,}\,+\,\frac{\,\left(\,s\,x\sqrt{\,l\,c\,}\,\right)^3\,}{3!}+\, \cdots\,\right]\;=\;\sqrt{\,\frac{l}{\,c\,}\,}\,\mathit{sinh}\left(\,s\,x\,\sqrt{\,l\,c\,}\,\right)\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-49179f27c35bd0d0135a9e248a71dd62_l3.png)
![Rendered by QuickLaTeX.com \begin{displaymath}C\;=\;\sum \psi_{2n-1}\;=\;\sqrt{\,\frac{\,c\,}{l}\,\left[\,s\,x\,\sqrt{\,l\,c\,}\,+\,\frac{\,\left(\,s\,x\,\sqrt{\,l\,c\,}\,\right)^3\,}{3!}\,+\, \cdots\,\right]\;=\;\sqrt{\,\frac{\,c\,}{l}\,}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-aa2c3768cf8bd9dbad5ee92796fefc84_l3.png)
Note that AD – BC = ![]()
That’s good for now. Next: T-Network Taylor Series Expansion
