I left off the last section ready to cascade the ideal transmission line model. The cascaded model appears as:
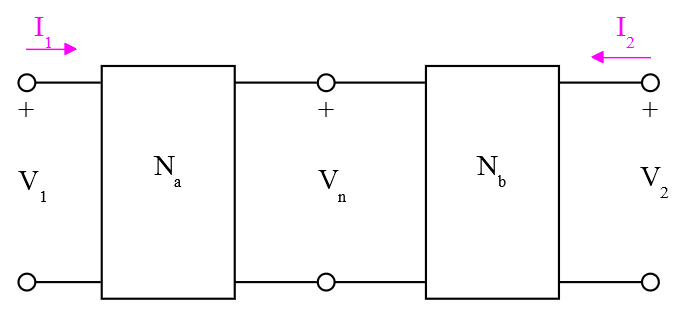
which may be described by:
![Rendered by QuickLaTeX.com \begin{displaymath}\left[ \begin{array}{c}V_1 \\ I_1 \end{array} \right]\;=\;\left[ \begin{array}{cc}A_a & B_a \\ C_a & D_a\end{array} \right]\;\left[ \begin{array}{cc}A_b & B_b \\ C_b & D_b\end{array} \right]\;\left[ \begin{array}{c}V_2 \\ -I_2 \end{array} \right]\;\;\Rightarrow\;\;\left[ \begin{array}{cc}A & B \\ C & D\end{array} \right]\;\left[ \begin{array}{c}V_2 \\ -I_2 \end{array} \right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-bb59a7431aecf266c06939521dcb3205_l3.png)
where

Making substitutions:
![Rendered by QuickLaTeX.com \begin{displaymath}\left[ \begin{array}{c}V(s,d) \\ -I(s,d) \end{array} \right]\;=\;\left[ \begin{array}{cc}\mathit{cosh}\left[\,\Gamma\,\right]\,d & Z_o\,\mathit{sinsh}\left[\,\Gamma\,\right]\,d \\ \frac{\,\mathit{sinh}\left[\,\Gamma\,\right]\,d\,}{Z_o} & \mathit{cosh}\left[\,\Gamma\,\right]\,d\end{array} \right]\;\left[ \begin{array}{c}V(s,0) \\ -I(s,0) \end{array} \right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-4fb83746094e08da5795bebae1dfbc3c_l3.png)
where the hyperbolic functions are defined:
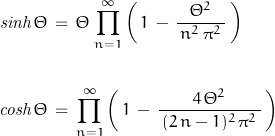
But it’s so much more convenient to use Mathematica to work through these functions …
The open and short circuit parameters of the uniform transmission line are given as:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}\left[ z_{i,j} \right]\;&=\;\frac{1}{\,Z_o\,}\,\left[ \begin{array}{cc}\mathit{coth}\left[\,\Gamma\,\right]\,d & \mathit{csch}\left[\,\Gamma\,\right]\,d \\ \mathit{csch}\left[\,\Gamma\,\right]\,d & \mathit{coth}\left[\,\Gamma\,\right]\,d\end{array} \right]\;\\\\\left[ y_{i,j} \right]\;&=\;Z_o\,\left[ \begin{array}{cc}\mathit{coth}\left[\,\Gamma\,\right]\,d & \mathit{csch}\left[\,\Gamma\,\right]\,d \\ \mathit{csch}\left[\,\Gamma\,\right]\,d & \mathit{coth}\left[\,\Gamma\,\right]\,d\end{array} \right]\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-9b5c51ef9b9af145326c6679b13a950c_l3.png)
The voltage and current expressions of this line having length d as a function of position x are given:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}V(s,x)\,&=\,V(s,d)\,\mathit{cosh}\left[\,\Gamma\,\right]\,(d-x)\,+\,I(s,d)\,Z_o\,\mathit{sinh}\left[\,\Gamma\,\right]\,(d-x)\\\\I(s,x)\,&=\,I(s,d)\,\mathit{cosh}\left[\,\Gamma\,\right]\,(d-x)\,+\,V(s,d)\,\frac{1}{\,Z_o\,}\,\mathit{sinh}\left[\,\Gamma\,\right]\,(d-x)\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-43d6cd7db017af5a7aa90b8bf2f38b7b_l3.png)
where again, ![]() and
and
![]()
An open-circuit output:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}V(s,x)\,&=\,V(s,0)\,\frac{\,\mathit{cosh}\left[\,\Gamma\,\right]\,(d-x)\,}{\mathit{cosh}\left[\,\Gamma\,\right]\,d}\\\\I(s,x)\,&=\,V(s,0)\,\frac{\,\mathit{sinh}\left[\,\Gamma\,\right]\,(d-x)\,}{Z_o\,\mathit{cosh}\left[\,\Gamma\,\right]\,d}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-2cc5a2eca01589e962b7b9f8242aa53e_l3.png)
and a short-circuit output:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}V(s,x)\,&=\,V(s,0)\,\frac{\,\mathit{sinh}\left[\,\Gamma\,\right]\,(d-x)\,}{\mathit{sinh}\left[\,\Gamma\,\right]\,d}\\\\I(s,x)\,&=\,V(s,0)\,\frac{\,\mathit{sinh}\left[\,\Gamma\,\right]\,(d-x)\,}{Z_o\,\mathit{sinh}\left[\,\Gamma\,\right]\,d}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-f0ee3bdaf9b0ece1d4938f9165214d08_l3.png)
If a voltage source having impedance ZS is applied at the input of a line of length d which has a load impedance ZL
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}V(s,x)\,&=\,V(s,0)\,Z_o\,\frac{\,Z_L\,\mathit{cosh}\left[\,\Gamma\,\right]\,(d-x)\;+\;Z_o\,\mathit{sinh}\left[\,\Gamma\,\right]\,(d-x)}{\,Z_o\,(Z_s\,+\,Z_L)\,\mathit{cosh}\left[\,\Gamma\,\right]\,d\,+\,(Z_s\,Z_L\,+\,Z_o^2)\,\mathit{sinh}\left[\,\Gamma\,\right]\,d\,}\\\\I(s,x)\,&=\,V(s,0)\,\frac{\,Z_o\,\mathit{cosh}\left[\,\Gamma\,\right]\,(d-x)\,+\,Z_L\,\mathit{sinh}\left[\,\Gamma\,\right]\,(d-x)}{\,Z_o\,(Z_s\,+\,Z_L)\,\mathit{cosh}\left[\,\Gamma\,\right]\,d\,+\,(Z_s\,Z_L\,+\,Z_o^2)\,\mathit{sinh}\left[\,\Gamma\,\right]\,d\,}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-d997af1a3f432d0be571f64aceccba11_l3.png)
This line has no distortion if R/L = C/G
Assume R = G = 0 (zero series resistance; infinite shunt resistance: perfect conductor, perfect insulator – lossless line)
The short-circuit admittance is
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}y_{11}\,=\,y_{22}\,&=\,\sqrt{\,\frac{\,C\,}{L}\,}\,\mathit{coth}\left[\,s\,d\,\sqrt{\,L\,C\,}\,\right]\;=\;\frac{1}{\,L\,d\,s\,}\,\prod_{n=1}^\infty\,\left[\,\frac{\,1\,+\,\frac{4\,L\,C\,d^2\,s^2}{\,(2\,n\,-\,1)^2\,\pi^2\,}\,}{1\,+\,\frac{\,L\,C\,d^2\,s^2\,}{n^2\,\pi^2}\,}\,\right]\\\\y_{12}\,=\,y_{21}\,&=\,-\sqrt{\,\frac{\,C\,}{L}\,}\,\mathit{csch}\left[\,s\,d\,\sqrt{\,L\,C\,}\,\right]\;=\;\frac{1}{\,L\,d\,s\,}\,\prod_{n=1}^\infty\,\left[\,\frac{1}{1\,+\,\frac{\,L\,C\,d^2\,s^2\,}{n^2\,\pi^2}\,}\,\right]\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-d40eea8b6fd2b838b36b400381e2fc0b_l3.png)
where the poles and zeroes are located:
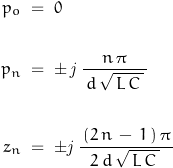
Lumped Parameters
For structures that may be represented with a number of identical sections, an iterated lumped structure can approximate the distributed structure when individual sections are small and the number of identical structures is large.
Consider the T section representation of an incremental lumped parameter network:
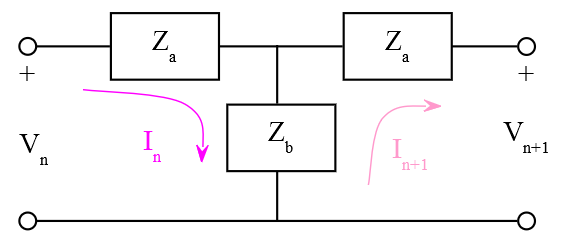
The mesh equations of this network are:
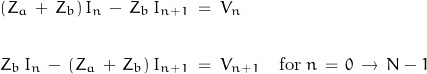
Re-arranging into matrix form:
![Rendered by QuickLaTeX.com \begin{displaymath}\left[ \begin{array}{c}V_{n+1} \\ I_{n+1}\end{array} \right]\;=\;\left[ \begin{array}{cc}1+\dfrac{Z_a}{Z_b} & -\left(\dfrac{Z_a^2}{Z_b}+2\,Z_a\right) \\ -\dfrac{1}{Z_b} & 1+\dfrac{Z_a}{Z_b}\end{array} \right]\;\left[ \begin{array}{c}V_n \\ I_n \end{array} \right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-502713e974a8c0eb60522f80e6c4692f_l3.png)
Configuring this expression in the form of:
![]()
The quantity ![]() is found from the eigen values of
is found from the eigen values of ![]() which are found from:
which are found from:
![]()
where I is the identity matrix.
The eigen values are related as:
![]()
Setting ![]() leads to
leads to ![]() and
and ![]()
Set ![]() which requires:
which requires:
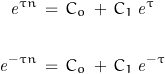
Solving for the constants C0 and C1:
![]()
A fair bit of pushing and pulling gives
![Rendered by QuickLaTeX.com \begin{displaymath}\left[ \begin{array}{c}V_n \\ I_n\end{array} \right]\;=\;\left[ \begin{array}{cc}\mathit{cosh}[n\,\tau] & -Z_b\,\mathit{sinh}[n\,\tau]\,\mathit{sinh}[\tau] \\ -\dfrac{\mathit{sinh}[\tau]}{Z_b\,\mathit{sinh}[\tau]} & \mathit{cosh}[n\,\tau]\end{array} \right]\;\left[ \begin{array}{c}V_o \\ I_o \end{array} \right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-cd7cdbf84855a19e878f61bafea39ef7_l3.png)
Since the short-circuit output voltage VN is 0, the input current is:
![]()
Within the intermediary sections
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}I_n\;&=\;V_o\,\frac{\mathit{cosh}[(N-n)\,\tau]}{Z_b\,\mathit{sinh}[N\,\tau]\,\mathit{sinh}[\tau]}\\\\V_n\;&=\;V_o\,\frac{\mathit{sinh}[(N-n)\,\tau]}{\mathit{sinh}[N\,\tau]}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-862a53f6ad1b1f292674379c3ccb494e_l3.png)
Since the open-circuit output current IN is 0, the input current is:
![]()
Within the intermediary sections
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}I_n\;&=\;V_o\,\frac{\mathit{sinh} [(N-n)\,\tau]}{Z_b\,\mathit{cosh}[N\,\tau]\,\mathit{sinh}[\tau]}\\\\V_n\;&=\;V_o\,\frac{\mathit{cosh}[ (N-n)\,\tau]}{\mathit{cosh}[N\,\tau]}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-10a45a0c2657a1931b9ee09d4be91586_l3.png)
For a N-section network:
![Rendered by QuickLaTeX.com \begin{displaymath}\left[ \begin{array}{c}V_N \\ -I_N\end{array} \right]\;=\;\left[ \begin{array}{cc}\mathit{cosh}[N\,\tau] & -Z_b\,\mathit{sinh}[N\,\tau]\,\mathit{sinh}[\tau] \\ -\dfrac{\mathit{sinh}[N\,\tau]}{Z_b\,\mathit{sinh}[\tau]} & \mathit{cosh}[n\,\tau]\end{array} \right]\;\left[ \begin{array}{c}V_o \\ -I_o \end{array} \right]\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-57d50267154940d52ee86e8869e76539_l3.png)
The short-circuit admittance parameters:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}y_{11}\;=\;y_{22}\;&=\;\frac{\mathit{cosh}[N\,\tau]}{\,Z_b\,\mathit{sinh}[\tau]\,\mathit{sinh}[N\,\tau]\,}\;=\;\frac{\mathit{coth}(N\,\tau)}{\,Z_b\,\mathit{sinh}(\tau)\,}\\\\y_{12}\;=\;y_{21}\;&=\;\frac{-1}{\,Z_b\,\mathit{sinh}[\tau]\,\mathit{sinh}[N\,\tau]\,}\;=\;-\frac{\mathit{csch}[N\,\tau]}{\,Z_b\,\mathit{sinh}[\tau]\,}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-a2ad629c9ab7e65bb4dbc7a0ca989172_l3.png)
For ease in pole-zero analysis, it is desired to express these relationships in factored form. Applying the expansions of the hyperbolic functions shown in an earlier post, the admittance parameters can be expressed as::
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}y_{11}\;=\;y_{22}\;&=\;\dfrac{\prod_{n=1}^N\left(\,\dfrac{Z_a}{\,Z_b\,}\,+\,1\,-\,\mathit{cos}\left[\,\dfrac{\,(2\,n\,-\,1)\,\pi\,}{2\,n}\,\right]\,\right)}{\;Z_b\,\left[\,\left(\,\dfrac{Z_a}{\,Z_b\,}\,+\,1\,\right)^2\,-\,1\,\right]\,\prod_{n=1}^{N-1}\left(\,\dfrac{Z_a}{\,Z_b\,}\,+\,1\,-\,\mathit{cos}\left[\,\dfrac{\,n\,\pi\,}{N}\,\right]\,\right)}\\\\y_{12}\;=\;y_{21}\;&=\;\dfrac{-1}{\;Z_b\,2^{N-1}\,\left[\,\left(\,\dfrac{Z_a}{\,Z_b\,}\,+\,1\,\right)^2\,-\,1\,\right]\,\prod_{n=1}^{N-1}\left(\,\dfrac{Z_a}{\,Z_b\,}\,+\,1\,-\,\mathit{cos}\left[\,\dfrac{\,n\,\pi\,}{N}\,\right]\,\right)}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-fe9b283f44eec54b7eb7fe2b5b608de5_l3.png)
For a lossless line:
![Rendered by QuickLaTeX.com y_{11}\;=\;y_{22}\;&=\;\dfrac{s\,C\,\prod_{n=1}^N\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,(2\,n\,-\,1)\,\pi\,}{2\,n}\,\right]\,+\,\dfrac{\,L\,C\,s^2\,}{2}\,\right)}{\;\left[\,\left(\dfrac{\,L\,C\,s^2\,}{2}\,+\,1\,\right)^2\,-\,1\,\right]\,\prod_{n=1}^{N-1}\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,n\,\pi\,}{N}\,\right]\,\right)\,+\,\dfrac{\,L\,C\,s^2\,}{2}\,}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-4ac6f3e39ea9d3a60ac3d39a34eea680_l3.png)
![]()
so that:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}y_{11}\;=\;y_{22}\;&=\;\dfrac{s\,C\,\prod_{n=1}^N\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,(2\,n\,-\,1)\,\pi\,}{2\,n}\,\right]\,+\,\dfrac{\,L\,C\,s^2\,}{2}\,\right)}{\;\left[\,\left(\dfrac{\,L\,C\,s^2\,}{2}\,+\,1\,\right)^2\,-\,1\,\right]\,\prod_{n=1}^{N-1}\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,n\,\pi\,}{N}\,\right]\,\right)\,+\,\dfrac{\,L\,C\,s^2\,}{2}\,}\\\\y_{12}\;=\;y_{21}\;&=\;\dfrac{-1}{\;2^{N-1}\,\left[\,\left(\dfrac{\,L\,C\,s^2\,}{2}\,+\,1\,\right)^2\,-\,1\,\right]\,\prod_{n=1}^{N-1}\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,n\,\pi\,}{N}\,\right]\,\right)\,+\,\dfrac{\,L\,C\,s^2\,}{2}\,}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-6be9b0899db2d6f222db8415ed78a1ef_l3.png)
For a distributed RC line,
![]()
and:
![Rendered by QuickLaTeX.com \begin{displaymath}\begin{align}y_{11}\;=\;y_{22}\;&=\;\dfrac{s\,C\,\prod_{n=1}^N\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,(2\,n\,-\,1)\,\pi\,}{2\,n}\,\right]\,+\,\dfrac{\,R\,C\,s\,}{2}\,\right)}{\;\left[\,\left(\dfrac{\,R\,C\,s\,}{2}\,+\,1\,\right)^2\,-\,1\,\right]\,\prod_{n=1}^{N-1}\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,n\,\pi\,}{N}\,\right]\,\right)\,+\,\dfrac{\,R\,C\,s\,}{2}\,}\\\\y_{12}\;=\;y_{21}\;&=\;\dfrac{-C\,s}{\;2^{N-1}\,\left[\,\left(\dfrac{\,R\,C\,s\,}{2}\,+\,1\,\right)^2\,-\,1\,\right]\,\prod_{n=1}^{N-1}\left(\,1\,-\,\mathit{cos}\left[\,\dfrac{\,n\,\pi\,}{N}\,\right]\,\right)\,+\,\dfrac{\,R\,C\,s\,}{2}\,}\end{align}\end{displaymath}](https://davemcglone.com/wp-content/ql-cache/quicklatex.com-f6b03745acb2cc0957a726bb258f2f18_l3.png)
with simple poles located at:
![]()
That’s good for now. Next: Non-Uniform Distribution
