Skin Depth & Coated Wire 4 Drift Velocity

Electrons wiggle. By definition, current is a measure of electron wiggle. If for no other reason, electrons wiggle when the temperature exceeds absolute 0 K. These electrons are bound to their atom so the wiggle in place. The motion is random and the net velocity is 0, so there is no current at the macro level but there is thermal noise current/voltage which is proportional to the square root of temperature.

In good conductors, there are free electrons floating around; collectively, they may be referred to as a “Fermi gas”. The electron Fermi velocity is much higher than the thermal velocity, but again, the motion is random and the net current is zero.

What is normally considered “electricity” is the movement of free electrons in the presence of an electric field: a battery is placed across a wire, electrons flow, the wire gets hot and melts. This movement of electrons is the drift velocity. It’s slow …

Copper (16.78 nΩ m) is the most common conductor: silver is better (15.87) but more brittle and … far more expensive. Furthermore, the difference from copper is relatively minor. Gold (22.14) is the third best. It is too soft … and way too far expensive – and rare – to be a feasible industrial grade conductor. Aluminum (26.5) is the 4th best but has issues; oxidation, thermal expansion, softer – more easily damaged. So copper it is.

In a gross sense, one can think of “electricity” as marbles in a straw: a marble can be placed slowly in one end of the straw but another comes out instantaneously.

The drift velocity of free electrons in copper may be determined with a bit of math; not much. Mostly.

The drift velocity is defined as:

$\begin{displaymath}\nu\;=\;\frac{I}{\,n\,A\,q\,}\end{displaymath}$

where I is the current, n is number of electrons, A is the area the electrons pass through, and q is the charge an electron carries.

Hm-m-m… number of electrons.

Copper density is 8.92 gm/cm³ with an atomic mass of 63.546 g/mol: So … 140,371 mol/m³

The Avogadro number states there are 6.022e23 atoms per mole so 1 m³ of copper contains 8.453e28 atoms/m³. Copper has one free electron per atom so there are 8.453e28 electrons/m³.

AWG#24 wire has a diameter of 0.511 mm; the area is therefore 205.084e-9 m²

Assume a current of 10 mA

$\begin{displaymath}\nu\;=\;\frac{I}{\,n\,A\,q\,}\quad\Rightarrow\quad\nu\;=\;\frac{0.01}{\,(8.453e28)\,(205.084e-9)\,(1.602e-19)\,}\;=\;3.6 \mu m/s\end{displaymath}$

An alternative means of determining drift velocity is directly related to the applied electric field:

$\begin{displaymath}\nu\;=\;V\,\frac{q\,\tau}{\,2\,d\,m_e\,}\end{displaymath}$

where V is the applied voltage, τ is the mean time between collisions, ℓ is the distance traveled, and $m_e$ is electron mass.
Let ℓ = 1m.

Need to determine τ which is related to conductivity.

$\begin{displaymath}\sigma\;=\;\frac{\,n\,q^2\,\tau\,}{m_e}\;\;\Rightarrow\;\;\tau\;=\;\frac{\,\sigma\,\m_e\,}{\,n\,q^2\,}\;\rightarrow\;\frac{\,(1\,/\,16.78)\times 10^{-9}\;9.11\times 10^{-31}\,}{\,(8.453e28)\,(1.602e-19)^2\,}\;=\;\textnormal{\small{25e-15}}\;s\end{displaymath}$

The drift velocity per volt is now calculated as:

$\begin{displaymath}\nu\;\frac{m/s}{\,V\,}\;=\;\frac{(1.602e-19)\,(25.03e-15)}{\,2\,(1)\,(9.11e-31)\,}\;=\;2.2\, mm/s/V\end{displaymath}$

whereas the speed of the electromagnetic wave is found to be:

$\begin{displaymath}\nu\;=\;\sqrt{\,\frac{\,2\,\omega\,}{\,\sigma\,\mu\,}\,}\;\;\Rightarrow\;\;\sqrt{\,\frac{\,2\,\times \,2\,\pi\,f\,}{\,(5.96e7)\,4\,\pi\times10^{-7}\,}\,}\;\;=\;\;0.4096\,\sqrt{\,f\,}\;\;=\;\;1295\,m/s\;@\;f\;=\;10MHz\end{displaymath}$

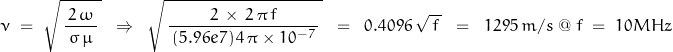
AWG#24

Material	Density g/cm³	Atomic Mass	Free Electrons/atom	# Free Electrons/mol ( $\times 10^{28}$ )	Drift Velocity (μm/s)/A
Cu	8.92	63.546	1	8.453	23.535
Ag	10.5	107.868	1	5.862	33.939
Ni	8.90	58.693	2	9.132	21.786

Previous: Part 3

Next: Part 5a

Leave a Comment Cancel Reply