Noise Equivalent Bandwidth

Noise in RC Networks is kT/C, not 4kTR $\Delta$ f

The thermal noise in a RC network is determined by the temperature and capacitance; resistance and frequency are not first-order factors.

Noise Equivalent Bandwidth (NEB)

Consider a 1st-order RC system … such as a passive detector with time constant as a basic parameter. Such a system may be represented in an electrical-equivalent form:

It is not uncommon for a shunt resistance to be known in such a detector. Having knowledge of a required time constant – perhaps 8 ms – the effective parallel capacitance can be derived.

(1) $\begin{equation*}\Re \; = \; \frac{1}{\, 1 + s \tau \,}\end{equation*}$

(2) $\begin{equation*}\tau \: = \: 8 ms \: = \: R \, C \quad \Rightarrow \quad C \: = \: \frac{8 ms}{450k} \: = \: 17.8 nF\end{equation*}$

The noise frequency response can be described as:

(3) $\begin{equation*}{V^2_{on,RMS}} \; = \; \int_{0}^{\infty} \frac{V^2_{DC,n}}{\; \left[ \: \sqrt{\: 1+(f/f_{3dB})^2 \:}\: \right]^2 \;}\; df\end{equation*}$

where $V_{DC,n}$ represents the low-frequency value of noise (often selected at 0.1 Hz)

Using the trig identity (or Mathematica):

(4) $\begin{equation*}{V^2_{on,RMS}} \quad = \quad \int \frac{1}{\:a^2 + u^2\:} \: du \quad = \quad \frac{1}{a}\: tan^{-1} \left( \frac{u}{a} \right)\: +\: K\end{equation*}$

Leads to the expression:

(5) $\begin{equation*}{V^2_{on,RMS}} \quad = \quad V^2_{DC,n} \:\: f_{3dB} \:\: tan^{-1} \left( \frac{f}{\;f_{3dB}\;} \right) \vert_{0}^{\infty} \:\: \Rightarrow \quad V^2_{DC,n} \:\: f_{3dB} \:\: \frac{\pi}{\;2\;}\end{equation*}$

where the 1st-order noise-equivalent-bandwidth (NEB) is defined:

(6) $\begin{equation*}NEB \quad = \quad f_{3dB} \:\: \frac{\pi}{\;2\;}\end{equation*}$

The RMS noise is determined with the NEB, not the system bandwidth.

(7) $\begin{equation*}{V^2_{on,RMS}} \quad = \quad \sqrt{\; V^2_{DC,n} \: f_{3dB} \: \frac{\pi}{\;2\;}\;} \quad = \quad \sqrt{\: V^2_{DC,n} \: NEB\:}\end{equation*}$

RC Noise

Consider a RC network as shown. Determine the thermal noise generated by such a network.
The capacitor is noise-less. The resistor has thermal noise associated with it; when included, the circuit may be rearranged as shown.

The thermal noise voltage now appears as a voltage source to an ideal impedance divider network.

(8) $\begin{equation*}vn \:\: = \:\: \sqrt{\; 4 \: k \: T \: R \: \Delta f \;}\end{equation*}$

The divider expression for an output across the capacitor is:

(9) $\begin{equation*}V_{out} \:\: = \:\: V_{in} \: \frac{Z_C}{\;Z_R + Z_C \;} \quad \Rightarrow \quad V_{on,rms} \:\: = \:\: \sqrt{\; 4 \: k \: R \: \Delta \;} \: \frac{\frac{1}{\: j \, \omega \, C \:}}{\;R + \frac{1}{\: j \, \omega \, C \:} \;}\end{equation*}$

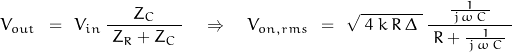
(10) $\begin{equation*}\qquad = \:\: \frac{\; \sqrt{\; 4 \: k \: T \: R \;}\; }{\; 1+j \frac{f}{\: f_{3dB} \:} } \qquad in \quad units \quad of \quad V^2/Hz\end{equation*}$

(11) $\begin{equation*}\sqrt{\; 4 \: k \: T \: R \;}\end{equation*}$

The magnitude of this expression is determined from

(12) $\begin{equation*}V^2_{on,rms} \:\: = \:\: \frac{\; 4 \: k \: T \: R \;}{\left| \; 1+j \frac{f}{\: f_{3dB} \:} \right|^2} \:\: = \:\: \frac{\; 4 \: k \: R \;}{\left[ \; \sqrt{\: 1 + \left( \frac{f}{\: f_{3dB} \:}} \: \right)^2 \; \right]^2 \;}\end{equation*}$

(13) $\begin{equation*}V^2_{on,rms} \:\: = \:\: \frac{\; 4 \: k \: T \: R \;}{\; 1 + \left( \frac{f}{\: f_{3dB} \:} \: \right)^2 \;}\end{equation*}$

The RMS noise is determined using the NEB

(14) $\begin{equation*}{V^2_{on,RMS}} \quad = \quad \sqrt{\: V^2_{DC,n} \: NEB\:} \quad = \quad \sqrt{\; V^2_{DC,n} \: f_{3dB} \: \frac{\pi}{\;2\;}\;}\end{equation*}$

Since $f_{3dB} = \frac{1}{\: 2 \, \pi \, R \' C \:}$ and $V^2_{DC,n} \: = \: 4 \: k \: T \: R \,$ :

(15) $\begin{equation*}{V^2_{on,RMS}} \quad = \quad \sqrt{\: 4 \: k \: T \: R \: \times \: NEB\:} \quad = \quad \sqrt{\: 4 \: k \: T \: R \: \times \: f_{3dB} \: \times \: \frac{\pi}{\;2\;}\;}\end{equation*}$

(16) $\begin{equation*}{V^2_{on,RMS}} \quad = \quad \sqrt{\: 4 \, k \, T \, R \: \times \: \frac{\pi}{\;2\;} \: \times \: \frac{1}{\: 2 \, \pi \, R \, C \:} \:} \quad \Rightarrow \quad \sqrt{\: \frac{\: k \, T \:}{C} \:}\end{equation*}$

Thermal noise is determined by capacitance in an RC-network. This has a significant effect on sampling networks.

Use the parallel RC network of the figure above. Assume warm room temperature (300K) and an $0.018 \mu$ F capacitor.

(17) $\begin{equation*}{V^2_{on,RMS}} \quad = \quad \sqrt{\: \frac{\: k \, T \:}{C} \:} \quad = \quad \sqrt{\: \frac{\: (1.38e-23) \, (300) \:}{18e-9} \:} \quad = \quad 480 \, nV\end{equation*}$

The RMS magnitude of a Gaussian noise distribution is equivalent to the 1- $\sigma$ level. The peak-to-peak value (V_pp) is roughly 6 – 7 times the RMS value or 2.88 $\mu$ V ( $\pm 1.44 \mu V$ ). The peak-to-peak magnitude represents the probability range of values; for $\sigma$ = 3.3, 1 sample out of 1000 will exceed the calculated magnitude (0.99903). At $\sigma$ = 3, 3 samples out of 1000 (0.9973) will exceed the calculated magnitude.

(This is picking at hairs to a certain extent. “Noise” is not fully analytical; at best, an analysis may provide reasonable limits but rarely an exact value. I fully expect to see about 10% more noise on a physical implementation than an ideal analysis would predict so it makes little sense to calculate noise magnitudes to more than 3 places … and that mainly to follow trends.)

For a 12-bit, 1V full-scale range (FSR) ADC, a least-significant-bit (LSB) is 244 $\mu$ V; it’s 15.3 $\mu$ V in a 16-bit converter.

If one were to calculate the noise based solely on the thermal noise of the resistance:

(18) $\begin{equation*}v_{on,rms} \:\: = \:\: \sqrt{\; 4 \: k \: T \: R \: \Delta f \;} \:\: \Rightarrow \:\: \sqrt{\; 4 \, (1.38e-23) \, (300) \, (450e3) \;}\:\: = \:\: 86 \, nV/\sqrt{\,Hz \,}\end{equation*}$

The RC network RMS noise voltage vs temperature

If a detector has a responsivity of 150 V/W, the SNR goes to 1 at an input stimulus of 3.2 nW. (SNR = 1 implies a signal level equal to the noise level – sometimes referred to as “minimum detectable signal”). If the detection bandwidth is say 20 Hz, SNR = 1 at 2.5 nW.

Of course, a physical detector would have other noise sources which would need to be considered in an actual system. This noise is inherent to the detector, it becomes part of the signal and is treated as such by later electronic networks such as amplifiers.

The significance of “3.2 nW” can only be determined in conjunction with the range of the desired measure of physical phenomenon: if the minimum desired measure is 32 nW, all is good – there’s $20 \, log (32/3.2) = 20 \,dB$ of signal head room. If 320 pW, there’s a problem. If 2.5 nW, there’s still a problem – my minimum signal is in the noise.

There was a wonderful “handbook” – over 1000 pages – of nothing but referenced mathematical relationships: Abramowitz and Stegun: “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.”

It’s easier to look everything up now though … but I’ve kept my copy.