Coax – Dave McGlone

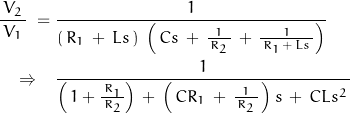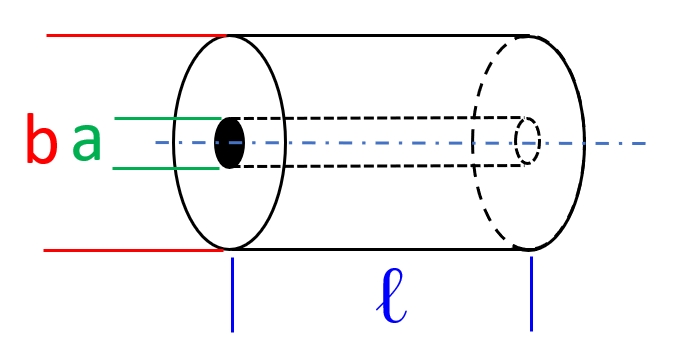
Coax Definitions

Capacitance

In somewhat formal terms, the capacitance of a coax structure is found by assuming a total charge Q on the center conductor and integrating over the resulting electric field to find the voltage between the conductors. The capacitance is the ratio of the charge to the potential. Ouch.

It becomes easier by assuming infinite length, no fringe fields, and constant geometry – the internal field is constant along the length. The center conductor is assumed positively charged; the potential is measured from negative conductor to positive conductor.

(1) $\begin{equation*}C \; = \; \frac{\, Q_t \,}{V} \; \end{equation*}$

and the charge per unit length l is:

(2) $\begin{equation*}\rho \; = \; \frac{\, Q_t \,}{l} \; \end{equation*}$

The electric field inside a coax structure having uniform charge density on the center conductor is identical to that of the electric field related to the same charge distributed on a line in free space.

The electric field directed along the r direction is found based on Gauss’ Law:

(3) $\begin{equation*}E \; = \hat{r} \; \frac{\, \rho_t \,}{\, 2 \pi \epsilon_r \, r \,} \; \end{equation*}$

The potential V is found by integrating:

(4) $\begin{equation*}V \; = - \, \int_c \; E \cdot dl \; \, \, = \, \, - \int_{r=b}^{a} \left( \, \hat{r} \frac {\rho_t}{\, 2 \pi \epsilon_r r \,} \right) \, \cdot \, \hat{r}\, d \rho\;\end{equation*}$

which – with a bit of manipulation – comes down to:

(5) $\begin{equation*}V \; = \; +\frac{\rho_t}{\, 2 \pi \epsilon_r \,} \, ln \left(\, \frac{b}{a}\, \right) \; \end{equation*}$

A bit of pushing and pulling on the expression gives:

(6) $\begin{equation*}C \; = \; \frac{\, 2 \pi \epsilon_o \, \epsilon_r \,}{ln \left( \frac{b}{\, a \,} \right)}\end{equation*}$

Inductance

A similar exercise is used to determine the inductance of a coax line. Using the same geometry and assumptions, assume a current I through the center conductor and integrate over the resulting magnetic field to obtain the resulting magnetic flux.

(7) $\begin{equation*}L \; = \; \frac{\, \Phi \,}{I} \; \end{equation*}$

The resulting magnetic intensity is found from:

(8) $\begin{equation*}H \; = \; \hat{\phi} \, \frac{\, I \,}{\, 2 \pi \, r \,} \, \, for \, a \leq r \leq b\; \end{equation*}$

Converting to magnetic flux density – easy enough, multiply H by $\mu$ :

(9) $\begin{equation*}B \; = \; \hat{\phi} \, \frac{\, \mu \, I \,}{\, 2 \pi \, r \,} \, \, for \, a \leq r \leq b\; \end{equation*}$

Now integrate over the surface to obtain $\Phi$ :

(10) $\begin{equation*}\Phi \; = - \, \int_S \; B \cdot dS \; \end{equation*}$

It might be noticed that this is equivalent to:

(11) $\begin{equation*}\Phi \; =; -\mu \, \int_S \; H \cdot dS \; \end{equation*}$

The magnetic field contained within a coaxial structure carrying current I is equivalent to the magnetic field of a line current I in free space

Expanding the integral:

(12) $\begin{equation*}\Phi \; = \; \int_{r=b}^{a} \, \int_{z=0}^{l} \, \left( \, \hat{\phi} \frac {\mu I}{\, 2 \pi r \,} \right) \, \cdot \, \hat{\phi}\, dr \, dz\;\end{equation*}$

Note that the inductance is only dependent on geometry and material – not current; a non-linear system.

Wiggling the expression around a bit gives a usable result:

For ideal coax inductance:

(13) $\begin{equation*}L \; = \; \frac{\, \mu \,}{2 \pi} \; ln \left( \frac{b}{\, a \,} \right) \; = \; 250 \, nH/m\end{equation*}$

By calculation: 251.4 nH

All of which is used to come up with the usable result:

The parameters depend on the geometry of the cable. A Belden RG-58 coax cable is built with AWG20 (33 mil) center conductor. Nominal impedance is 52 $\Omega$ . The resistance of the center conductor is 32.81 $\Omega$ \ km – or about 10 m $\Omega$ per foot. Capacitance is rated at 28.5 pF/ft.

a = radius of center conductor = 33/2 mil = 419 $\mu$ m
b = radius of dielectric = 116/2 mil = 1473 $\mu$ m
$\epsilon_o$ = permittivity (8.8542e-12 F/m)
$\epsilon_r$ = relative permittivty (= 1 for $\epsilon_o$ )
$\mu_o$ = permeability (4 $\pi$ 10e-7 H/m) $\approx$ 1.25664e-6 H/m
$\mu_r$ = relative permeability (= 1 for non-magnetic environments)

For ideal coax capacitance:
The dielectric material is polyethylene with $\epsilon_r$ = 2.25

(14) $\begin{equation*}C \; = \; \frac{\, 2 \pi \epsilon_o \, \epsilon_r \,}{ln \left( \frac{b}{\, a \,} \right)} \; = \; 100 \, pF/m\end{equation*}$

By calculation: 99.6 pF

(15) $\begin{equation*}L \; = \; \frac{\, \mu \,}{2 \pi} \; ln \left( \frac{b}{\, a \,} \right) \; = \; 250 \, nH/m\end{equation*}$

By calculation: 251.4 nH

Impedance

The impedance of this cable is defined by:

(16) $\begin{equation*}Z \; = \; \frac{1}{2 \pi} \; \sqrt{\, \frac{\mu}{\, \epsilon \,}}\, ln \left( \frac{b}{\, a \,}\right) \; \Rightarrow \; 50.25 \, \Omega\end{equation*}$

This may be approximated as:

(17) $\begin{equation*}Z \; = \; \frac{\, 59.96 \,}{\, \sqrt{ \epsilon_r \,}}\, ln \left( \frac{b}{\, a \,}\right) \; \Rightarrow \; \frac{138.1}{\sqrt{\, \epsilon_r \,}}\, log \left( \frac{b}{\, a \,}\right)\end{equation*}$

Start with the 2nd-order passive filter of an earlier post.

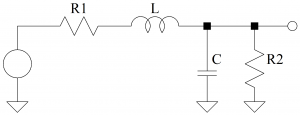
which is described with the expression …

(18) $\begin{equation*}\begin{align}\frac{V_2}{\,V_1 \,} \; = \; &\frac{1}{\left( \, R_1 \, +\, L s \,\right) \; \left( \, C s \, + \, \frac{1}{\, R_2 \,} \, + \, \frac{1}{ \, R_1 \, + \, L s \,} \right)} \\\quad \Rightarrow \quad &\frac{1}{\left( \, 1+ \frac{R_1}{\, R_2 \,} \right) \, + \, \left( \, C R_1 \, + \, \frac{1}{\,R_2\,} \, \right) s \, + \, C L s^2 \,}\end{align}\end{equation*}$

Leave a Comment Cancel Reply