Atmospheric CO2 – Avalanche Photodiodes (APD)

Photodiode Operation

The photodiode detector provides the conversion from optical power to electrical current; it is this electrical current which is eventually turned into “numbers” to be analyzed.

Consider the basic pn-junction (diode). An electric field establishes a depletion region in which no free carriers exist. When a photon of the correct energy correctly impacts an atom in this region, it is converted into an electron-hole pair by means of energy transfer (keeping in mind that the negatively-charged electron breaks its orbital bond to become a free carrier and leaves an energy “hole” behind. The positively-charged hole effectively acts as a free charge carrier). The electric field causes the now-free carriers to move towards one potential region or the other. This movement of charge-carriers is a current which is proportional to the number of photons absorbed in the detection region. Of course, practical considerations prevent this idealized operation.

The current created by the movement of a single electron being quite small – by definition, (1 q/s ~ 6.2 aA = 6.2E-18 A) – it is often desired to amplify this signal within the detector itself. One method of achieving this is by designing the detector diode to operate in avalanche mode whereby the charge carrier has enough energy to break multiple additional carriers from their orbital bonds. Operation in avalanche mode borders on a potentially-destructive region – care must be taken to assure correct external biasing.

Proper design and external control can allow the detection of single photons … although that is not the focus of this project, it is useful to know the possibility as a lower limit of the feasible.

The APD is strongly dependent on bias voltage and temperature (and manufacturing techniques – which are not of concern here). Small-signal measurements require tight control of both.

The operational regions of a representative diode are shown not quite to scale: (the reverse-bias region to the left of zero is compressed; the positive voltage region covers about 0 to 2V).

A photodiode generally operates in the reverse-bias region; the APD operates within the “avalanche knee” region. The point of this illustration is to demonstrate the sensitivity of the detector to excessive bias voltages – a slight over-voltage can cause a condition of destructive over-current.

It is recommended that this specific detector be limited to 10V bias and 1mA current (per pixel).

Noise

The lower limit of sensitivity of a photodiode is limited by the noise of the detector itself at small signal levels or by photon noise at high multiplication factors.

The detector detection limit is often set by the “dark current”; the current that flows through the detector in the absence of photon excitation. This occurs from random fluctuations in the detector lattice due to thermal energy and crystalline defects. This noise is often small enough that it has a Poisson distribution rather than Gaussian.

Shot noise is caused by the random crossing of charge across a potential barrier such as a pn-junction. It is defined as:

$i_{n,shot}\;=\;\sqrt{\,2\,q\,I+{dk}\,f\,}$

where q = electric charge constant = 1.602E-19 C ; f is frequency bandwidth in Hz ; and I_dk is dark current in C/s

Although this representation of shot noise does not show temperature dependency, the number of free carriers making up the magnitude of dark current is.

As a point of reference, a discrete quantity of approximately 300 represents the limit where the Gaussian Distribution begins to be an acceptable approximation of the Poisson. A movement of 300 electrons per second is approximately equivalent to a current of 2fA. This detector is noisier than this so the Gaussian representation is acceptable. Very sensitive detectors may have lower currents than this.

The avalanche effect adds an additional component to the dark current. There is a component of leakage current that is due to surface effects such as crystal boundary defects which is not subject to the avalanche multiplication effect and a volumetric component which is.

A simplistic expansion of the expression for dark current depends on:

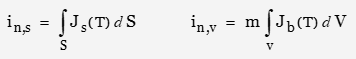
where factor m represents the multiplication effect and the current density factors are dependent on the physical dimensions of the structure.

Finer details involve doping levels and manufacturing processes and add little to this discussion.

Taking into account the excess noise factor, the dark current may now be expressed as:

$I_{dk}\;=\;i_{n,s}\,+\,m\,i_{n,v}$

But the avalanche process itself is noisy – all those carriers banging around transferring energy add a significant amount of noise to the detector. This noise is a function of the ionization process and becomes a statistical property based on the ratio of hole to electron ionization probabilities which is far beyond the purpose of this discussion.

A formal expression for the multiplication factor is dependent on many factors: location of absorption, temperature, and whether majority carriers are holes or electrons are primary considerations.

Without delving into the complexities, the expression[1] for electron charge carriers is given as

This is sometimes presented as a noise factor NF

The noise factor decreases with lower k_eff and m

Impact ionization requires a large electric field. An electron can become so highly energized by the field that it can create an electron-hole pair by colliding with a lattice electron in the valence band and bumping it up to the conduction band.The generation rate due to impact ionization is expressed as:

The coefficients a_n and a_p are not equal or constant and are dependent on the applied electric field

The ionization ratio k is a function of the bias voltage – which generates the E-field within the detector whose characteristics are dependent on the junction doping parameters. The photon absorption is a function of distance travelled and photon energy – which is proportional to wavelength

$E_p\;=\;\nu\,\dfrac{h}{\,\lambda\,}$

where n is the velocity of the photon, h is Planck’s constant (h = 6.626E-34 J×s), and $\lambda$ is the wavelength of the photon.

The noise factor expression is sometimes approximated as

$NF\;=\;2\,+\,m\,k_{eff}$

which can be misapplied as $\gamma$ is gain-dependent

Taking into account the excess noise factor, the dark current is now expressed as

$I_{dk}\;=\;i_{n,s}\,+\,i_{n,v}\,\left[\,\left(\,2\,m\,-\,1\,\right)\,+\,k_{eff}\,\left(\,m\,-\,1\,\right)^2\,\right]$

where i_n,s is the contribution due to surficial currents and i_n,v is the contribution due to volumetric currents.

[1] Mclntyre,R.J., “Multiplication Noise in Uniform Avalanche Diodes”,
IEEE Trans. Electron Devices, ED13, pp. 164-168 (1966)

Signal Current

The signal current is expressed as:

$I_{sig}\;=\;m\,P_o\,\mathcal{R}(\lambda)$

where P_o is the photon power applied to the detector in Watts and Â(l) is the responsivity of the detector as a function of the photon wavelength l. Typical values for Â(l) at the wavelength of sensitivity are on the order of 9-11 A/W

While the wavelength dependency may not be an issue for a single wavelength of photon, the responsivity to wavelengths within the detector other than that desired may contribute to signal degradation – or may affect the signal magnitudes of multiple desired wavelengths of equal intensity.

The avalanche process adds noise to the signal in the same manner as the bulk component of the dark current. The signal current is a bulk effect…

In the absence of photonic excitation

i.e., the dark current…

While the expression looks deliciously complex when expanded and re-stated, the complexity of the signal and noise interaction could be taken as an indication that the APD structure is not suitable for precise measurements in spite of the increased gain.

But that involves a different discussion…

Signal-to-Noise Ratio

An acceptable expression for signal-to-noise ratio can be presented as

If a bulk factor is defined as $bf\;=\;2\,m\,-\,1\,+\,k\,(\,m\,-\,1\,)^2$ , then:

Signal Current: $I_{sig}\;=\;m\,P_o\,\mathcal{R}(\lambda)$

Shot Noise: $i_{n,s}\;=\;\sqrt{\,2\,q\,I_{dk}\,f\,}$

Avalanche Noise Effect: $i_{n,av}\;=\;\sqrt{\,2\,q\,i_{bulk}\,bf\,f\,}$

Signal Noise: $i_{n,sig}\;=\;\sqrt{\,2\,q\,I_{sig}\,bf\,f\,}$

So that the expression for SNR may be presented as:

… which is not particularly usable for more than an illustration of the interactions within the detector …

So – on to the specific detector (actually an array but this discussion will concentrate on a single diode unless noted)

The Detector

Photodetectors may be constructed from many different materials: silicon is common for visible light and near-infrared wavelengths. In this discussion, a photodetector constructed of a mercury-cadmium-tellerium (HgCdTe … or “mer-cad”) alloy.

It should be noted that the detector discussed was “proposed” for an actual project. It was deemed not suitable but is presented as an example of “not-good” as opposed to everything is “fine and dandy”. Not everything in engineering woks as projected; sometimes the engineer’s job is to justify rejection.

This specific detector has “gain” of 1000 with dark current of 300 pA/cm³ at 12V bias (dark current decreases with lower voltage; capacitance increases)

A 2×2 pixel array forms the receiving focal plane in the manner illustrated

The GRN area represents the focused beam. Assume a beam of uniform intensity is exactly lined up with the pixel corners as shown. If each of 4 pixels measures $64\times 64\,\mu m$ with a $5\,\mu m$ trace between them, the diagonal distance (optimal beam diameter) is:

$d_{diag}\;=\;(\,2\,\times\, 64\,)\,+\,(\,1\,\times\, 5\,)\,\sqrt{\,2\,}\;\approx\;188\,\mu m$

The area of the beam is $\pi\,\left(\,\frac{\,188\,}{2}\,\right)^2\;\Rightarrow\;27.8\times 10^3\,\mu m^2$

If the entire pixel is active area, then only 16.4 mm² is receptive to photons:
… only 59% of the beam strikes the detectors

Array construction details are not directly part of the signal stream but have an effect on the signal processing requirements and detection limitations.

The bond pads and traces of this detector (not counting diode capacitance) combine for an effective capacitance of 2.2pF and trace resistance of about 20 $\Omega$ .

The voltage noise at 82K over 1MHz is $v_{n,RMS}\;=\;8.25\,\mu V\,;\;\;v_{n,pp}\;=\;49\,\mu V$

The minimum current noise under the same conditions is $i_{n,RMS}\;=\;388\,pA\,;\;\;i_{n,pp}\;=\;2.3\, nA$

This severely limits the usable dynamic range. It should be noted that the 1 MHz bandwidth is not sufficient for the desired application.

The detector electron efficiency is about 0.7 at the desired wavelength of 1570 nm. Under the ideal conditions determined herein, the overall effective detection efficiency is approximately 0.4.

If a Gaussian distribution is assumed (as implied), then the pixel response variation of 1 $\sigma$ = 2.3% at V_bias = 12V gives a peak-to-peak variation of ±6.9%. This adds a degree of amplitude uncertainty that will exceed the magnitude resolution desired.

Empirical Test Results

Single pixel dark current measurements at different temperatures

As expected, the dark current has a strong dependency on temperature. Also as expected, the dark current is also strongly dependent on the bias voltage.

The slope of dependency is sufficient at the recommended bias voltage of 10V to be sensitive to small variations in bias voltage. As a rough approximation, the slope of the change in dark current at a bias of 10V appears to be about 2.1pA/V.

This plot compares the change of output current under different illumination conditions. The dark current is the lower BLU response. The GRN response is at the wavelength of interest; the RED curve could represent an OFF-band wavelength. (The RED and GRN responses are almost fully super-imposed). The CYAN curve is at the limit of response.

The manufacturer recommends a maximum current of 1uA

The slope lines used for signal and dark current are identical within the limits of this chart resolution at roughly 1 decade/3V. At 10V, the SNR is 40dB … but note the signal current exceeds the recommended limit.

The manufacturer claims a dark current of 13pA at V_bias = 10V. This should result in a dark current of 208pA for a 4×4 array

This measurement obviously includes post-detection processing but assuming linearity, it appears that within the wavelength range of interest, there is a linear relationship between responsivity and temperature.

The question arises:

Is anything gained by operating at LN77?

Doesn’t look so based on this information … and much complexity (and error sources) could be eliminated by dropping the cryogenic requirement.

Ideal voltage noise is proportional to the square-root of temperature ( $v_n\;=\;\sqrt{\,4\,k_B\,R,T,\Delta f\,}$ ). With all other factors held constant, the difference in noise due to temperature is

$\sqrt{\,T\,}\bigg|_{77K}\;=\;8.775\qquad\sqrt{\,T\,}\bigg|_{273K}\;=\;16.5$

About a doubling of thermal voltage noise between liquid nitrogen-cooled and 0C if all else is equal. A proper evaluation needs to consider “external” noise contributions of each temperature. And cost. Physical and monetary.

Stability of temperature is usually more important than absolute value.

Comparison

This does not indicate an endorsement; it indicates a similar representative device for comparison.

This photodiode has roughly the same attributes as the DRS detector of interest – but as a single diode rather than an array. The biggest difference is the much larger bias voltage required and a much larger bandwidth than the DRS device

The Excelitas C30645

80 um active area 45-95V (~5000 um²)

1550 nm peak sensitivity (1100 – 1700 nm) at 1GHz bandwidth

spec’d at 9.3A/W at 1550nm

(but response curve indicates better than this: 10.9A/W at 1570 nm)

QE_min = 75% m_min = 10 m_max = 20

The gain is less – but “gain” isn’t as important as the absolute value of signal to be measured

The maximum dark current for this diode is listed as 50 nA at gain = 10

For comparison, the measured dark current for the DRS array with 16 pixels was 100 nA

The C30645 is rated at 5 mA_max (although I would suspect non0linearity at this level). Still, if one assumes a max signal of 100uA, the available dynamic range of the C30645 is approximately

whereas the DRS dynamic range is measured at about 40 dB

Both signal ranges are well within feasible electronic processing range.

Relating required laser power depends on many assumptions regarding optics. The DRS detector consists of square pixels with 4 detectors per pixel. The fill factor needs to be determined. If the optics match the circular detector of the C30645, then working backwards would require detected laser power to generate a signal of 10x I_dk of

$Q_E\,\mathcal{R}\,P\;=\;10\,I_{dk}\;\;\Rightarrow\;\;0.75\,\times\,11\,\times\,P\,=\,10\,\times \,50\,nA\;\;\Rightarrow\;\;P\;=\;60\,nW$

If all else were equal, the DRS array would require 60/0.59 = 102 nW to receive the same signal: if by “same signal”, one intended to mean the same SNR, this would increase to

$Q_E\,\mathcal{R}\,P\;=\;10\,I_{dk}\;\;\Rightarrow\;\;0.75\,\times\,11\,\times\,(\,P/0.59\,)\,=\,10\,\times \,100\,nA\;\;\Rightarrow\;\;P\;=\;1700\,nW$

Considerations of signal strength, noise level, optical efficiency, and supporting hardware all make the single detector a more optimal choice than an array structure.

Cooling

To achieve high-resolution, lowering the noise floor is desired. This floor is primarily defined by “dark current” – aka, “reverse leakage current” in a “normal” diode (pn-junction). The primary components of reverse leakage current are thermal an shot noise – both of which are proportional to the square root of temperature in degrees Kelvin. Note that is is the temperature of the junction, not the package or “ambient”. Lowering the device temperature is the most direct means of decreasing dark current (other factors are related to the actual construction of the device)

Liquid nitrogen is often used as a means of lowering the photodiode. This temperature is roughly 77K.

“room temperature” is usually defined as 25°C = 298.15K … call it 300K

$\sqrt{\,77\,}\;=\;8.775\;;\quad\sqrt{\,300\,}\;=\;17.321$

In theory, the dark current should be reduced by a factor of 2 (all else remaining constant). This gain needs to be considered in light of issues involved with cryogenic cooling.

A discussion of the interface networks is a side issue covered on a branch off this topic.

That’s a wrap for this topic.

Next: Ranging Radar

Back 9: Photodiodes & Signal Range

Up: Articles

Circuit Discussion: Photodiode As Signal Source

Noise

Signal Current

Signal-to-Noise Ratio

Leave a Comment Cancel Reply